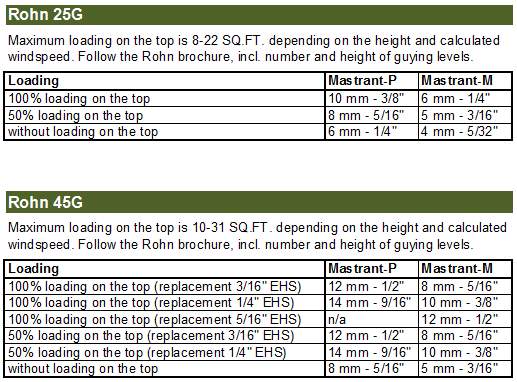
Consejos & Recomendaciones
Consejos y trucos útiles

Esta guía general le mostrará cómo establecer eficazmente la longitud necesaria del cable de anclaje, tensarlo y asegurarlo para una instalación a largo plazo.
El procedimiento es adecuado tanto para la instalación de mástiles sencillos como para grandes sistemas de antenas con torres de celosía.
- Desenroscar el tensor hasta la máxima longitud.
- Instalar el tensor en el anclaje.
- Enhebrar la cuerda a través del ojo/dedo superior.
- Instale el tensor de la cornamusa en su extremo libre. Utilice CL234 para cuerdas de 6 a 11 mm (1/4" a 1/2") o CL223 para cuerdas de 3 a 6 mm (1/8" a 1/4").
- Ajuste la longitud deseada del cable de anclaje o ajuste su longitud gradualmente. Ventajosamente, se puede utilizar un tensor de cornamusa, y su fácil deslizamiento en la cuerda. El procedimiento será diferente según el método de instalación del mástil/torre y de los cables de sujeción (elevación del mástil plegado desde el suelo, extensión gradual del mástil telescópico, instalación del mástil en partes, ...).
- En la posición de trabajo (antes del tensado final), la parte tensora debe tener un aspecto similar al siguiente:


- Una vez completado el ajuste, tense la cuerda con un tensor de cornamusa.
- Instale la abrazadera de la cuerda y apriétela firmemente:


- Ahora puede soltar el tensor de la cornamusa y atar al menos 2 nudos de seguridad (doble medio nudo):

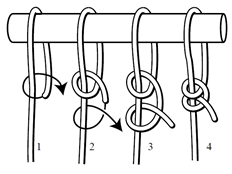
- Apriete los nudos firmemente y asegure el extremo libre de la cuerda con cinta de cable (para cuerdas de hasta aproximadamente 5 mm - 3/16 ") cuerdas o instalar una segunda abrazadera de seguridad.
- Tensar el cable de sujeción a la tensión requerida utilizando un tensor:


- Apriete firmemente los tensores de la cuerda. Si utiliza tensores con tuercas de seguridad (como el Tensor Mandíbula-Mordaza en la foto), apriete también estas tuercas.
- Antes de empezar, lea nuestros artículos Principios breves de Anclar con las Cuerdas Sintéticas y Procedimiento de Instalación Recomendado.

Sugerencia de sustitución de los cables de acero por cables sintéticos Mastrant - basada únicamente en la resistencia!
| Acero (1570 Mpa) | P | M |
| 4 mm (5/32") | 6 | 4 |
| 5 mm (3/16") | 8 | 5 |
| 6 mm (1/4") | 10 | 6 |
| 7 mm (9/32") | 12 | 8 |
| 8 mm (5/16") | 14 | 10 |
| 9 mm (11/32") | - | 12 |
| 10 mm (3/8") | - | 12 |
| Galvanizado EHS | P | M |
| 5 mm (3/16") 1x7 | 10 | 6 |
| 6 mm (1/4") 1x7 | 14 | 8/10 |
| 8 mm (5/16") 1x7 | - | 12 |

Al diseñar un "sistema de anclaje" (la cuerda de anclaje con terminales, elementos de conexión y sujetadores), es necesario tener en cuenta una serie de factores:
- La fuerza del sistema está dada por la fuerza del elemento más débil. Por lo tanto, es inútil utilizar un cable de 50 kN con un tensor de 5 kN.
- Incluso la cuerda sintética más perfecta es elástica - extendiéndola se prolonga. En el diseño del mástil y su anclaje (así como cuando la antena está atada), es necesario contar con esta propiedad y siempre evaluar la influencia sobre la extensión de la estructura de la prolongación del sistema de anclaje. Para algunas situaciones, se necesitará una cuerda más fuerte (con menor estiramiento absoluto) de lo que sería necesario para una construcción diferente que a la que no importala prolongación de las anclas. El problema se produce principalmente donde el punto de anclaje (Ground anchor point) está demasiado cerca a la base de la torre (Tower base), o cuando es un mástil enrejado (Lattice tower) anclado firmemente con baja elasticidad. Siempre es recomendable realizar un cálculo de control de cuánto tiempo el sistema de anclaje se alargará a la carga máxima elegida y luego evaluar cómo este alargamiento afectará a su construcción o estabilidad.
- La cuerda debe estar protegida de cualquier borde afilado. Por esta razón es necesario terminar la cuerda con un guardacabos o atar a un elemento de conexión (Coupler) con la superficie plana. Aquí hay que tener en cuenta que los materiales metálicos inadecuados corroen, poniendo su superficie áspera. ¡Nunca atamos la cuerda directamente a los pilares o piedras de hormigón! Si queremos utilizar como punto de anclaje de tierra una piedra, una roca o una columna de hormigón, recomendamos utilizar un lazo de la cuerda de acero a la que unimos la cuerda de anclaje con un elemento de conexión liso.
- Muy peligrosa para una cuerda es una fricción de cualquier objeto en su camino (por ejemplo, ramas, piedras, partes de edificios ...). Incluso la cuerda estirada se mueve en el viento y este movimiento puede causar que la cuerda se rompa. Especialmente solapado (y por lo tanto peligroso) es la fricción de las ramas de los árboles. Éstas se a menudo mueven muy intensamente, si la cuerda se frota de la rama, casi seguramente será dañada dentro de unos días. Si utiliza para fijar las antenas los árboles, se recomienda utilizar la cuerda de acero en el punto de flexión sobre las ramas y tensar la cuerda sintética con una polea.
- La parte inferior del sistema de anclaje debería formar un anudo de acero con una longitud de 2-4 m (Steel rope cord). Éste asegura que la cuerda sintética no roa ningún animal ni lo dañe la actividad humana (inconsciente o consciente).
Clave de la seguridad es el extremo de la cuerda:
- La cuerda de anclaje puede ser terminada con un guardacabos con grapa (instalación permanente) o atada a un objeto liso

- Para sujetar la cuerda apretándola, se recomienda que la cuerda no se mueva contra el objeto al que está atada (aunque es un punto de fijación liso). Esto se puede asegurar atando una cuerda al elemento de conexión – eslabón rápido (Chain quick-acting coupler), un mosquetón o un grillete (Shackle) - y despues lo uniremos al punto de la fijación.

- Detrás del sujetacable principal (el justo detrás del guardacabos) se necesita asegurar el extremo libre de la cuerda por un elemento de seguridad – un sujetacable segundo o varios lazos, similar al enganche de anclaje (Anchor hitch). El extremo de la cuerda libre se asegura firmemente contra el aflojamiento, por ejemplo, mediante una correa apratadera de cable (Cable tie).


- Otra opción es usar sujetacables prensados. Sin embargo, es práctico utilizar sólo un extremo de la cuerda, de lo contrario no sería posible modificar su longitud. Los vendemos como una "cuerda con terminaciones" o "cuerda con un guardacabos" - here.

- Al tensar, el diámetro de la cuerda se reduce y así se libera del sujetacable. Por esta razón, los sujetacables se deben apretar cuando la cuerda esté tensada, es decir, "bajo carga".
- ¡Cuidado con los perrillos clásicos (Bull-dog grip)! Estos sujetacables de cuerda diseñados para cuerdas de acero pueden "cortar" la cuerda sintética durante un grado de apriete alto. En cualquier caso, no los recomendamos usarlos como los sujetacables principales de la terminación de la cuerda - pueden ser utilizados como un sujetacable "de seguridad" detrás del sujetacable principal.
- Le recomendamos que considere el terminal en angulo. Aunque estos sujetacables son bastante caros, tienen varias características excepcionales - son las más guardosos para la cuerda, por tensar se aprietan y permiten un cambio cómodo en la longitud del sistema de anclaje.

Errores y causas de accidentes más comunes:
- El punto de anclaje está demasiado cerca de la base del mástil y por lo tanto el ángulo de la cuerda de anclaje y el mástil es mucho más pequeño que 45 °.
- Los sujetacables no son apretadas cuando se aprieta el cable.
- No hay ningún elemento de seguridad detrás de los sujetacables (segunda sujetacable, nodo).
- La cuerda no termina con un guardacabos pero está atada inapropiadamente.
- La cuerda roe el animal o corta el vándalo.
- En el caso siguiente, se utilizó una cuerda con una gran elongación


- Contamos o medimos la longitud de anclaje necesaria ("sistemas de anclaje").
- Añadimos la longitud necesaria para crear la terminación. Para la terminación estándar (guardacabos, sujetacables, nudo) es aproximadamente 60 veces el diámetro de la cuerda en cada lado.
- Cortamos la cuerda con un objeto caliente con un borde adecuado (por ejemplo, una punta de soldadura). La temperatura de fusión del poliéster es de aproximadamente 260◦C, fibras de Dyneema de 150◦
- Preparamos un guardacabos apropiado. Si es necesario, podemos estirar el guardacabos con unos alicates, enhebrar al objeto al que va a sujetar el ancla y volver a su forma original de nuevo. Pequeñas deformaciones de la forma de guardacabos no afectan la resistencia resultante.
- Preparamos un sujetacable adecuado que desarmamos antes de la instalación.
- Sujetemos la cuerda alrededor del guardacabos, colóquamosla en el sujetacable y montamoslo (vea la imagen). Dejamos el extremo libre de la cuerda de longitud de 35 veces de su diámetro detrás del sujetacable (para crear un nodo de seguridad).

- Coloquamos el sujetacable cerca del guardacabos – por apretar entre la abrazadera y los extremos conectados de la cuerda. 2.
- Apretamos firmemente el sujetacable y formamos un nudo (vea la imagen). Aseguramos firmemente el extremo libre de la cuerda con la correa de apretamiento a los cables contra el desenrollado

- Los sujetacables se deben apretar repetidamente cuando se aprieta la cuerda. El extremo de la ancla, que no será accesible después del apretamiento, debe ser apretado antes de instalarlo. Fijamos el guardacabos al punto fijo y apretamos gradualmente la cuerda en varios pasos. Después de cada aumento de la fuerza de apriete, apretamos los tornillos del sujetacable. Idealmente, hacemos el último apriete cuando se alcanza la carga de trabajo máxima (30% de resistencia). Sin embargo, para las cuerdas más fuertes, este ideal es difícil de conseguir - el apretamiento se realiza, por ejemplo, cargando la cuerda apretada entre dos puntos fijos perpendicularmente a su eje, por ejemplo, mediante un vehículo o un aparejo provisional.
- Fijamos el ancla al lugar donde se va a usar. Lo estiramos gradualmente y apretamos los sujetacables (vea punto anterior).
- Comprobamos visualmente que la cuerda no se deslizó en el sujetacable - de ser así, significa que no hemos seleccionado el procedimiento adecuado de estirar y apretar, o que el sujetacable está defectuoso.
- Para tensar la cuerda podemos usar los tensores de rosca. En el caso de los mástiles telescópicos, los tensores no son imprescindibles - bajamos ligeramente el mástil (parte relevante), apretamos los sujetacables y luego lo volvemos a una posición estable - la idoneidad de este procedimiento es, por supuesto, diferente para cada tipo de mástil.
- La tensión óptima de la cuerda depende de varios factores – la construcción y la resistencia del mástil, el tipo y la resistencia de la cuerda, la distancia del base del mástil desde el punto de anclaje. En la mayoría de las aplicaciones, la fuerza del 5-20% de la resistencia de la cuerda es la mejor.
- Después de la tensión final de las anclas al "estado inactivo", la cuerda se "asentará" durante algún tiempo. Revisamos las anclas y, si es necesario, apretamos al día siguiente después de la instalación y luego aproximadamente 3 veces después de 1 semana. Siempre tenemos que seguir el procedimiento de apriete correcto!
Errores y causas de accidentes más comunes:
- El punto de anclaje está demasiado cerca de la base del mástil y por lo tanto el ángulo de la cuerda de anclaje y el mástil es mucho menor que 45 °.
- Los sujetacables no son apretados cuando se aprieta la cuerda.
- No hay ningún elemento de seguridad detrás de los sujetacables (segundo sujetacable, nodo).
- La cuerda no termina con un guardacabos pero está indebidamente atada.
- La cuerda roe el animal o la corta el vándalo.
Martin Huml, OL5Y/OK1FUA,
(nota: todas las tablas están disponibles en formato Excel)
Durante mis actividades de radioaficionado, dedico la mayor parte de mi tiempo (probablemente como cualquiera de nosotros) a la cuestión de las antenas. Y una de las tareas más importantes, y quizás la más difícil, es conseguir que la antena "esté en el aire" y mantenerla allí. Aparentemente esto se aplica a todas las antenas, quizás con la excepción de las antenas de bebidas... Escribí sobre este tema en el artículo "Cómo construir y guy mástiles de antena simples" (revista "Radioamatér" 2 & 3/2004). En aquel momento, ya me pareció que este tema es tan interesante, complicado y extenso que sería conveniente volver a él.
Otro motivo para escribir el siguiente artículo fue incluir las preguntas que me hacían mis amigos o que surgían por su cuenta, por ejemplo: "¿Por qué se sujeta la vertical tan abajo?", "¿Será esta cuerda lo suficientemente fuerte?", "¿Podrá este mástil llevar la antena?", etc. La mayoría de las veces no pude encontrar una respuesta mejor que "porque creo que es suficiente" o "porque lo vi así en algún sitio". Esto no parece muy científico. La práctica y la experiencia son estupendas e insustituibles, pero demasiadas cosas son conjeturas, así que cuando mis actividades me llevaron al "guying", decidí estudiarlo también desde el punto de vista teórico. En primer lugar, me gustaría decir que no soy ingeniero; así que, después de estudiar un tiempo, consulté al ingeniero Richard Beber, que, a diferencia de mí, ha estudiado este tema. En este sentido, me gustaría darle las gracias: el artículo no se habría escrito si no fuera por él.
Por lo tanto, como indica el nombre de este artículo, su tema principal se centra en la forma de guyar las antenas. Esto no significa que los propietarios de los mástiles autoportantes no encuentren algo interesante. Por ejemplo, los cálculos de las fuerzas que actúan sobre la antena con el viento u otras cuestiones podrían ser útiles.
Términos utilizados y simplificación
Pido indulgencia a los expertos y lingüistas: uso estos términos tal y como los conozco en la práctica de los aficionados:
- Lugar (punto) de montaje = el lugar donde se monta (fija) la cuerda de sujeción en el mástil
- Altura de montaje = la distancia entre el punto de montaje y la base del mástil (base, etiquetada como HKI
- Punto de anclaje (punto de arriostramiento) = el lugar en el que el cable de sujeción se fija al suelo (u otro punto fijo)
- Distancia de arriostramiento = la distancia entre el punto de arriostramiento y la base del mástil (base, etiquetada como RKI)
- El sistema = el mástil con la antena
Una antena vertical es en realidad un mástil sin la antena. Por lo tanto, cuando no sea apropiado en el texto siguiente, no distinguiré entre estos dos tipos de antenas. En otras palabras, por ejemplo, la frase "tensar en medio del mástil" deberá entenderse como "tensar en medio de la vertical".
A menos que se indique lo contrario, asumimos que el mástil está construido sobre una superficie horizontal; por lo tanto, los puntos de sujeción en el suelo y el fondo del mástil están al mismo nivel, perpendicular al eje del mástil. Esto es para simplificar - la realidad tiende definitivamente a ser diferente. Por lo tanto, el siguiente texto indicará cómo tratar con la realidad.
En nuestras consideraciones, tampoco nos ocupamos del comportamiento de la propia antena - suponemos que la antena en el mástil no cambia.
Y, por último, para los que no son amigos de la física - hablaremos mucho de la fuerza, cuya unidad es 1 N (Newton). Por ejemplo, si levantas un peso de 1 kg, la fuerza que actúa sobre ti es de aproximadamente 10N.
La antena y el mástil
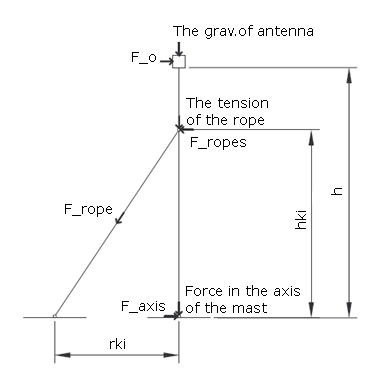
Si observamos el modelo simplificado del mástil atirantado y la antena en su parte superior (fig. 1), las siguientes fuerzas afectarán al sistema:
- fuerza de gravedad (masa del mástil, cuerdas y antenas),
- fuerza del viento resistente,
- Fuerza de tensión de los cables de sujeción.
Este conjunto de fuerzas producirá una reacción para que las fuerzas resultantes se equilibren. La reacción aparecerá en el agarre de la base del mástil y en los lugares de montaje de los cables de sujeción. También se producirá una deformación flexible del mástil y de los cables. En este sentido, no consideramos la deformación irreversible o la destrucción del material - son estos casos los que queremos evitar y por lo tanto nos centraremos en la identificación de todas las fuerzas actuantes.
Pero las fuerzas no representan todos los factores que van a influir en el comportamiento del sistema. No debemos olvidar la estructura del mástil (tubo, estructura de celosía, etc.) y el material del que está hecho, especialmente sus propiedades físicas como la densidad (peso específico), la flexibilidad y la resistencia. Del mismo modo, debemos conocer las propiedades de los cables de sujeción: su resistencia y su alargamiento. Resumamos lo que necesitamos saber:
- antena - masa
- antena - forma (número, longitud y diámetro de los elementos)
- mástil - estructura, material
- Cuerda de hombre - alargamiento (estiramiento con carga de trabajo), resistencia
Y los parámetros con los que vamos a tratar son los siguientes:
- altura total (la altura de la antena sobre el suelo = la altura del mástil)
- el número de direcciones de retenida (3 o 4)
- el número de niveles de arriostramiento (en cuántos niveles se arriostrará el mástil)
- la altura de la(s) fijación(es) del cable de sujeción
- la distancia del punto de arriostramiento desde la base
La distancia del arriostramiento
La primera cuestión que abordaremos es la influencia de la distancia del atirantado en la magnitud de las fuerzas (que actúan sobre el mástil y los cables de sujeción). Dividiremos esta tarea en las siguientes situaciones marginales: en el primer caso, el viento sopla desde la dirección de los tirantes; en el segundo caso, el viento sopla "entre los tirantes". (fig. 2)
Si el viento sopla desde la dirección del punto de arriostramiento, se trata de una simple composición de fuerzas - el caso de un triángulo rectángulo donde uno de los catetos es el mástil (h), el segundo la distancia entre la base del mástil y el punto de arriostramiento (r), donde la cuerda de arriostramiento es la hipotenusa (l). La proporción en que se encuentran los distintos catetos de este triángulo es la proporción de las fuerzas que actúan en las distintas direcciones. Sabemos (podemos calcular) la fuerza Fant causada por el viento que actúa sobre la antena. (Su valor específico no es importante en este momento; lo trataremos más adelante, ya que ahora estamos evaluando la influencia de la distancia del punto de amarre). Así pues, la fuerza sobre el mástil (en su eje) es Fst = Fant * h / r, y la fuerza que actúa sobre el cable de sujeción es Fko = Fant * l / r. Calcularemos la longitud de la cuerda por el Teorema de Pitágoras: l = √(h2 + r2).
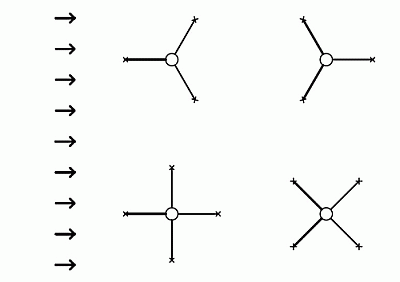
Cuando el viento sopla desde la dirección del eje entre los cabos la situación es algo más complicada, porque hay que tener en cuenta el ángulo entre los cabos, es decir, hacia cuántas direcciones está arriostrado el mástil.
direcciones de retencion
Para ello, miramos el mástil desde arriba e introducimos un total de 3 puntos: el mástil y 2 puntos de amarre. Además, introduciremos la dirección desde la que sopla el viento: es el eje entre los puntos de amarre que atraviesa el mástil. El lugar donde este eje se cruza con la línea de conexión entre los dos puntos de amarre es un punto que representa el punto de amarre virtual para el cálculo de las fuerzas actuantes. Vemos que está mucho más cerca de la base del mástil que la distancia de arriostramiento - cuanto más cerca esté, mayor será el ángulo entre los tirantes.
Se trata de nuevo de un caso de triángulos, pero no necesariamente de triángulos rectos. Si aplicamos las funciones goniométricas básicas llegamos a estas relaciones:
Para 4 tipos en 90°:
Fst = Fant * (h / r) * √2 = Fst = Fant * (h / r) * 1,414
Fko = Fant * (l / r) * (√2) / 2 = Fant * (l / )r * 0,707
para 3 tipos 120° cada uno:
Fst = Fant * (h / r) / cos(60/180π) = Fant * (h / r) / 0,5
Fko = Fant * (l / r) / cos(60/180π) = Fant * (l / )r .
A primera vista, es posible que no vea una característica interesante: cuando se atiranta en 3 direcciones, la fuerza que actúa sobre la cuerda de atirantado es la misma que con el viento "desde el atirantado" así como "entre las cuerdas de atirantado".
Cómo se ve esto en la práctica
Desde la perspectiva teórica, que probablemente sea aburrida para la mayoría de nosotros, pasamos a los efectos prácticos. (Prometo que el siguiente texto será sin fórmulas - serían mucho más complicadas...)
Para ilustrar, he elegido un ejemplo simple - un mástil de 10 m de altura con un tribanda (10/15/20m) en la parte superior. Repito de nuevo - es un ejemplo para mostrar el impacto de la distancia de guying y el número de direcciones a las que el mástil está guyed.
Por lo tanto, no estamos interesados en las propiedades del mástil o de la cuerda. Por lo tanto - dejamos que el viento sople sobre el tribanda a 130 km/h. Se puede calcular aproximadamente que la fuerza que actúa el viento es de aproximadamente 775N. Cómo he llegado a este resultado se explicará en el próximo capítulo; por ahora este resultado será suficiente.
Sin embargo, mencionaré un hecho muy importante, a saber, que la fuerza es proporcional a la velocidad al cuadrado (por ejemplo, la mitad de la velocidad = la cuarta parte de la fuerza; la fuerza en el caso de 80 km/hora será, por tanto, de aproximadamente 290 N). Sin embargo, la fuerza crece a un ritmo similar - por lo que se puede entender entonces lo que puede hacer un tornado con su velocidad de viento que alcanza más de 300 km/h en su centro, así que por favor no piense que los coches que vuelan por el aire son una mera invención de los cineastas americanos.
Pero ahora volvamos al tema de los vientos. En las siguientes tablas se puede ver la fuerza calculada para ambas versiones de arriostramiento (3 y 4 direcciones) y para el arriostramiento de 10 y 5 m. Creo que es obvio que acercar los puntos de arriostramiento al mástil resulta en un aumento innecesario de las fuerzas actuantes. Esto es similar en el caso del arriostramiento en 3 direcciones, que aumenta la carga en el mástil.
| Alto de la fijación | 10 m | ||
| Distancia de los puntos de amarre | 10 m | ||
| Velocidad del viento | 130 km/h | ||
| Dirección del viento | número de direcciones | Fuerza [N] que actúa: | |
| cable de sujeción | mástil | ||
| de la dirección del cableado | 4 | 1 095 | 775 |
| entre el cable de sujeción | 4 | 775 | 1 095 |
| de la dirección del cableado | 3 | 1 095 | 775 |
| entre el cable de sujeción | 3 | 1 095 | 1 245 |
| Alto de la fijación | 10 m | ||
| Distancia de los puntos de amarre | 5 m | ||
| Velocidad del viento | 130 km/h | ||
| Dirección del viento | número de direcciones | Fuerza [N] que actúa: | |
| cableado | mástil | ||
| de la dirección del cableado | 4 | 1 732 | 1 549 |
| entre el cableado de la cuerda | 4 | 1 224 | 2 191 |
| de la dirección del cableado | 3 | 1 732 | 1 549 |
| entre el cableado | 3 | 1 732 | 3 098 |
Como se puede ver, con una disposición razonable, las fuerzas causadas por un viento tan fuerte no son tan grandes. Como se puede encontrar en muchos lugares, incluso una cuerda relativamente débil resistirá si se designa para este propósito. Los lugares más débiles son todas las juntas ... Y en nuestras condiciones, no hay que olvidar las situaciones en las que la antena está encajada con la escarcha... Pero esto es realmente una distracción aquí y vamos a volver a ella.
Sólo para completar, un párrafo más - los lectores observadores han notado definitivamente que no se trata de la altura y la distancia absolutas - obtendremos los mismos resultados con mástil de 20m y la distancia de 20 y 10m. Se trata del ángulo formado entre el cable de sujeción y el mástil. Esto debe tenerse en cuenta especialmente en situaciones en las que el punto de amarre no puede colocarse en un nivel perpendicular al mástil (está en una pendiente). En este caso, por ejemplo, si tiene que colocar el punto de amarre 3 m más bajo que la base del mástil y quiere mantener el ángulo entre la cuerda y el mástil a 45°, tendrá que colocar el punto de amarre a 13 m del eje del mástil (¡cuidado, no desde la base del mástil!). Esto apenas se puede calcular, por eso es posible calcular y medir la longitud del cable de amarre - en este caso siendo 13*1,41 = 18,3m (1,41 = √2).
Fuerza del viento
Si colocamos un objeto en la corriente de un fluido, en nuestro caso el aire, provocará una resistencia por los elementos de fricción y presión. Esta resistencia se determina experimentalmente en los túneles de viento aerodinámicos y se expresa en relación con la fuerza de resistencia:
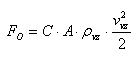 ,
,
Donde FO es la fuerza de resistencia [N], C es el coeficiente de resistencia del objeto (-), A es la superficie del objeto perpendicular a la dirección del viento [m2], ρvz es la densidad del aire [kg/m3], &vvz es la velocidad del viento [m/s].
El valor del coeficiente de resistencia no es constante, sino que depende del llamado número de Reynold - criterio adimensional, que expresa la relación entre la inercia y la viscosidad
Re = vvz * d / v ,
Donde d es la dimensión característica [m] a v es la viscosidad cinemática del aire.
Si simplificamos la antena (en nuestro caso un tribander) a varios cilindros, entonces la dimensión característica es el diámetro y Re equivale aproximadamente a 104 en condiciones normales mientras que el coeficiente de resistencia del objeto C es aproximadamente 1,2. Por la fuerza de resistencia que actúa sobre la antena (diámetro del tubo d = 35 mm, longitud l = 23.6 m, velocidad del viento vvz = 36 m/s = 130 km/h; densidad del aire 1.2 kg/m3) podemos determinar:
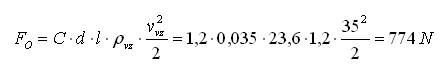 .
.
Esta fuerza actúa como una carga continua en toda la antena (si simplificamos la situación real en el mismo perfil de velocidad para toda la superficie de la antena). Podemos determinar la fuerza de resistencia que actúa sobre el mástil de forma similar.
La siguiente tabla ilustra las fuerzas calculadas para varias antenas típicas (pido disculpas a aquellos que no puedan encontrar su antena exacta en la tabla, por favor, sólo extrapolen).
| Antena | Área de viento [m2] | Fuerza del viento [N] a la velocidad como [km/h] | ||
| 50 | 130 | 180 | ||
| HF - 3el. tribander ECO | 0,82 | 116 | 765 | 1476 |
| HF - 3el. tribander A3S | 0,40 | 56 | 373 | 720 |
| HF - 3el. tribander TH3JRS | 0,32 | 45 | 299 | 576 |
| HF - 7el. tribander TH7DX | 0,88 | 124 | 821 | 1584 |
| HF - 11el. 5-bander TH11DX | 1,17 | 165 | 1092 | 2106 |
| HF - 10el. LP 10-30m LP1010 | 1,49 | 210 | 1390 | 2682 |
| HF - 5el. for 6m F9FT | 0,13 | 18 | 121 | 234 |
| HF - 5el. for 10m LJ105CA | 0,37 | 52 | 345 | 666 |
| HF - 5el. para 15m LJ155CA | 0,49 | 69 | 457 | 882 |
| HF - 5el. para 20m LJ205CA | 0,84 | 119 | 784 | 1512 |
| HF - 6el. para 20m HD OWA | 1,80 | 254 | 1680 | 3240 |
| HF - vertical 6-20m R6000 | 0,14 | 20 | 131 | 252 |
| HF - vertical 6-40m R8 | 0,24 | 34 | 224 | 432 |
| HF - Inv.V tamaño completo 20-160m | 0,90 | 127 | 840 | 1620 |
| 2m - 9el. 2M9 | 0,12 | 17 | 112 | 216 |
| 2m - 11el. F9FT | 0,18 | 25 | 168 | 324 |
| 2m - 12el. 2M12 | 0,14 | 20 | 131 | 252 |
| 2m - 17el. F9FT | 0,29 | 41 | 271 | 522 |
| 2m - 18el. 2M18XXX | 0,30 | 42 | 280 | 540 |
| 70cm - 18el. 440-18 | 0,08 | 11 | 75 | 144 |
| 70cm - 21el. 440-21ATV | 0,12 | 17 | 112 | 216 |
| 70cm - 38el. 432-13WLA | 0,24 | 34 | 224 | 432 |
| 23cm - 35el. 23CM35EZ | 0,06 | 8 | 56 | 108 |
¿Qué pueden causar las heladas?
La helada, que es un elemento muy importante en nuestros cálculos, que afecta a la función (así como a la supervivencia) de la antena, provoca
- aumento de la superficie los efectos del viento y
- ganancia de masa.
Como no tengo ninguna experiencia personal con las heladas, he consultado este tema con algunos amigos que tienen sus antenas en diversos lugares problemáticos, incluidos aquellos en los que las heladas duran varios meses. Su experiencia indica que la escarcha en los componentes añade hasta un 50-100 % y en casos extremos hasta un 200 % a su diámetro original (el componente aumenta entonces su diámetro). Veamos cuánto aumenta esto la carga del viento.
El capítulo anterior muestra que la fuerza de resistencia del viento es directamente proporcional a la superficie de la antena perpendicular a la dirección del viento y, por tanto, al diámetro de sus componentes. Así, si el diámetro de los componentes aumenta 2 veces, se duplica la fuerza del viento. Son cálculos muy sencillos: si quieres diseñar un sistema de antena para heladas extremas, multiplica las fuerzas por 3.
La cuestión de la masa es más complicada. Para su cálculo, necesitamos conocer no sólo el espesor de la escarcha, sino también su densidad. Aunque la densidad del hielo es de 917 kg/m3, la densidad de la escarcha indicada en la literatura y las normas se considera de 400-500 kg/m3 - calculemos preferentemente 500 kg/m3. Dado que nos interesa el aumento de la masa de la antena estacionaria, también necesitamos conocer la densidad del material del que está hecha. Normalmente se trata de una aleación de aluminio cuya densidad es de unos 2800 kg/m3.
Una breve observación sobre el cálculo: para simplificar, volveremos a considerar una antena formada por tubos o varillas. La masa del objeto m = V * ρ, donde V es el volumen y ρ la densidad. El volumen del cilindro es V = π * r2 * l, donde r es el radio y l la longitud. Si sustituimos los valores conocidos calcularemos la masa original y la masa de la escarcha. Esto se demuestra a continuación.
| Diseño del elemento /boom | Multiplicación del peso con el glaseado: | ||
| 50% | 100% | 200% | |
| Spar (todos los diámetros) | 1,2 | 1,5 | 2,4 |
| Tubo ø 8 mm, pared 1 mm | 1,5 | 2,2 | 4,3 |
| Tubo ø 10 mm, pared 1 mm | 1,6 | 2,5 | 5,0 |
| Tubo ø 14 mm, pared 1 mm | 1,8 | 3,0 | 6,4 |
| Tubo ø 24 mm, pared 1 mm | 2,4 | 4,4 | 9,9 |
| Tubo ø 24 mm, pared 2 mm | 1,7 | 2,8 | 5,7 |
| Tubo ø 30 mm, pared 1 mm | 2,7 | 5,2 | 12,1 |
| Tubo ø 30 mm, pared 2 mm | 1,9 | 3,2 | 6,7 |
| Tubo ø 50 mm, pared 1 mm | 3,8 | 7,8 | 19,2 |
| Tubo ø 50 mm, pared 2 mm | 2,5 | 4,5 | 10,3 |
Los datos mostrados en la tabla pueden resultar chocantes para algunas personas. ¡No es fácil admitir que la antena formada, por ejemplo, por tubos de 24 mm de diámetro con una pared de 1 mm aumente su masa en una helada del 100% en 4,4 veces! Por otro lado, hay que tener en cuenta que las condiciones para crear una helada continua en todo el perímetro del tubo, especialmente en los de mayor diámetro, son relativamente raras en los QTH ordinarios.
Como curiosidad, la Wikipedia dice lo siguiente sobre las heladas:
La escarcha es un fenómeno atmosférico que se desarrolla creando cristales de hielo en la superficie del objeto infligiendo los siguientes efectos:
• congelación de pequeñas gotas de la humedad del aire (nubes, niebla, etc.) en su contacto con la superficie del suelo, objeto u otros sujetos a la temperatura de 0°C y menos;
• precipitación (sublimación) de la humedad del aire sobre una superficie del suelo o sujetos suficientemente fríos y que incluso sin la presencia de niebla o nubes.
La mayor probabilidad de creación de escarcha se produce con el contacto a una temperatura (de 0 a -4 °C) entre la superficie del objeto y la corriente de aire húmedo. Con una temperatura inferior a -4 °C la posibilidad de creación de escarcha disminuye y a temperaturas inferiores a -12 °C la escarcha no se produce o es muy débil.
Los datos anteriores son interesantes sobre todo en la consideración de la estructura & diseño de la antena - hasta qué punto los componentes y el brazo deben ser dimensionados y reforzados para evitar la flexión. Este es un tema completamente diferente.
La próxima vez, nos centraremos en el tensado de un mástil real, incluyendo consideraciones sobre su resistencia y otros elementos que influyen.

Martin Huml, OL5Y/OK1FUA,
En la primera parte hablamos de las fuerzas y de las cuestiones relacionadas con el arriostramiento en general; hoy hablaremos del propio mástil. Antes de empezar me gustaría agradecer todos vuestros comentarios, preguntas y demás temas. Me alegro de que os haya interesado el artículo anterior e intentaré que siga siendo así.
En esta secuela nos centraremos en la versión más básica: el mástil tubular atirantado en un nivel por debajo de la antena. Esta situación se ilustra en la figura 1. Para simplificar los cálculos, supondremos que todo el mástil tiene el mismo diámetro de tubo y las mismas propiedades en toda su longitud. También supondremos que la velocidad del viento a lo largo del mástil es la misma (en realidad es menor justo por encima del suelo).

Al analizar las cantidades y propiedades que afectan al comportamiento del sistema llegamos a esta lista:
- la altura total del mástil, la altura de la cuerda fijada, la distancia del ancla a la base del mástil (para determinar las fuerzas que afectan al sistema)
- diámetros exterior e interior del tubo (para determinar la resistencia y el peso del mástil)
- propiedades físicas del material del que está hecho el tubo: densidad, módulo elástico, límite de resistencia, límite proporcional (para determinar la resistencia y el peso del mástil)
- área y peso de la antena (para determinar la fuerza de resistencia al viento)
- coeficiente de resistencia del mástil y de la antena (para determinar la fuerza de resistencia al viento)
- propiedades del entorno (aire): viscosidad cinética, aceleración de la gravedad, densidad del aire
- velocidad del viento
Salidas de los cálculos que deseamos obtener:
- fuerza en el eje de la base del mástil (acción sobre el punto de colocación de la base del mástil)
- fuerza en el eje de la cuerda (para la selección de la cuerda adecuada)
Sin embargo, nos interesará especialmente la seguridad - si el mástil sobrevivirá y con qué grado de seguridad.
Pero ¿cómo evaluar y comparar la seguridad si no tiene unidad y su expresión en palabras es bastante difícil y sobre todo subjetiva? Probablemente no podremos medirla. Los sectores de la construcción utilizan una unidad llamada coeficiente de seguridad. Se calcula de forma diferente para cada tipo de estructura, pero su interpretación (sentido) es siempre la misma: Si es mayor que 1, "hay una garantía teórica de que la estructura sobrevivirá". El valor mínimo recomendado es 1,4. Si la seguridad de la estructura implica varios factores, el coeficiente se calcula para cada factor por separado y la seguridad total de la estructura es la menor de ellas. En nuestro caso, hay dos factores críticos: la resistencia del material del que está hecho el mástil (es decir, la tensión en él), y el pandeo del mástil (para que el mástil no se doble). Nuestras consideraciones darán lugar a la evaluación de la seguridad total del sistema.
De lo anterior se desprende que hay un gran número de cantidades que son diferentes para situaciones específicas. Cada uno tiene una antena diferente, un mástil diferente, una altura de mástil diferente... A modo de ilustración, he elegido varias situaciones que me parecen adecuadas para la demostración y para las que he calculado diferentes resultados. En cada caso he elegido la altura de la fijación de la cuerda para que la seguridad total sea la mayor. Las variaciones individuales son las siguientes:
- La altura del mástil de 13 m, en el que se coloca una antena ECO (3el. tribander para 10/15/20m). Esta versión está calculada para 3 mástiles diferentes: tubo de diámetro 80 mm con pared de 3 mm de espesor de un duraluminio de calidad media (ver. A), tubo del mismo material 100/4 mm (B) y tubo de acero 60/3 mm (C).
- La altura del mástil de 13 m con antena de 11el. para una banda de 2 m en dos versiones: duraluminio medio de 60 mm de diámetro con una pared de 2 mm de espesor (D) y fibra de vidrio de 60 mm de diámetro con una pared de 5 mm de espesor (E).
- La última versión es un mástil de 23 m con una voluminosa antena TH7DX (7el. tribander para 10/15/20m) de nuevo en 2 versiones: duraluminio de alta calidad de 100 mm de diámetro con una pared de 10 mm de espesor (F) y acero de 100 mm de diámetro con una pared de 5 mm de espesor (G).
Otros parámetros utilizados para los cálculos son: densidad del aire = 1,2 kg/m3, aceleración de la gravedad = 9.82 m/s2, velocidad del viento = 36 m/s = 130 km/h, coeficiente de resistencia del mástil y de la antena C = 1.2. Los resultados se muestran en el cuadro nº. 1.
| Cantidad | Símbolo | A | B | C | D | E | F | G | Unit | |
| 11m duralumin ECO | 11m duralumin ECO |
11m steel ECO |
11m duralumin 11el. 2m | 11m fibra de vidrio11el. 2m | 23m duralumin TH7DX |
23m aceroTH7DX |
||||
| mástil - tubo | ||||||||||
| altura total | h | 13 | 13 | 13 | 13 | 13 | 23 | 23 | m | |
| altura de fijación de la cuerda | h_ki | 12 | 12 | 12 | 11 | 9 | 17 | 20 | m | |
| distancia del tipo | r_ki | 10 | 10 | 10 | 10 | 10 | 15 | 15 | m | |
| diámetro exterior | D_o | 80 | 100 | 60 | 60 | 60 | 100 | 100 | mm | |
| diámetro interior | D_i | 74 | 92 | 54 | 56 | 50 | 80 | 90 | mm | |
| densidad del mástil | ro_s | 2700 | 2700 | 7850 | 2800 | 1200 | 2800 | 7850 | kg/m3 | |
| módulo elástico | E_s | 60000 | 60000 | 200000 | 60000 | 18000 | 60000 | 200000 | MPa | |
| límite de fuerza | sigma_t | 300 | 300 | 320 | 300 | 220 | 350 | 320 | MPa | |
| límite proporcional | sigma_tu | 200 | 200 | 120 | 200 | 200 | 200 | 120 | MPa | |
| reacción de la cuerda | F_ropex | 1355 | 1486 | 1223 | 629 | 768 | 2446 | 2079 | N | |
| reacción en el fondo del mástil | F_fuerzas en el eje del mástil | 2023 | 2346 | 2153 | 856 | 858 | 4951 | 5808 | N | |
| reacción en el fondo del mástil perpendicular | F_axis | -381 | -492 | -270 | -267 | -128 | -376 | -743 | N | |
| fuerza en el eje de la cuerda | F_cuerda | 2116 | 2321 | 1911 | 934 | 1034 | 3697 | 3466 | N | |
| antena | ||||||||||
| área de la antena | S_ant | 0,82 | 0,82 | 0,82 | 0,18 | 0,18 | 0,9 | 0,9 | m2 | |
| peso de la antena | m_ant | 15 | 15 | 15 | 3,5 | 3,5 | 40 | 40 | kg | |
| evaluar la seguridad | ||||||||||
| tensión en el mástil | k_t | 4,01 | 6,21 | 2,86 | 2,37 | 2,14 | 3,16 | 3,34 | ||
| pandeo | k_b | 2,47 | 5,84 | 3,62 | 2,01 | 1,89 | 3,27 | 4,75 | ||
| seguridad total | k | 2,47 | 5,84 | 2,86 | 2,01 | 1,89 | 3,16 | 3,34 | ||
En la versión (A) quería mostrar que, aunque se utiliza un tubo relativamente grueso, la seguridad total no es tan perfecta como algunos podrían esperar basándose en su experiencia. Esto se debe a que la disposición del sistema con una sola altura de tirante no es, sin duda, óptima y exige mucho al material del mástil. Hablaremos de otras versiones la próxima vez, pero puedo revelar que la resistencia del sistema en doble arriostramiento es cuatro veces mayor e incluso nueve veces mayor en niveles de arriostramiento triple (por supuesto, si se colocan en alturas óptimas). También he incluido la versión (E) porque he visto mástiles similares utilizados por varios radioaficionados.
| material | density | módulo elástico | límite de fuerza | límite proporcional |
| kg/m3 | MPa | MPa | MPa | |
| duralumin | 2800 | 60000 | 180-450 | x |
| aluminum | 2700 | 60000 | 60-150 | x |
| acero | 7850 | 200000 | 320-835 | 120-290 |
| fibra de vidrio | 1200 | 18000 | 220 | x |
Tabla nº 2: propiedades físicas de los materiales
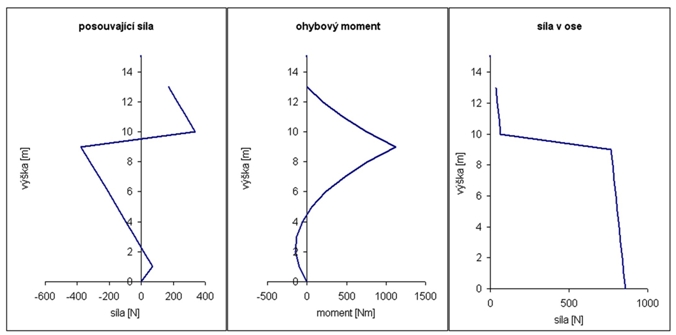
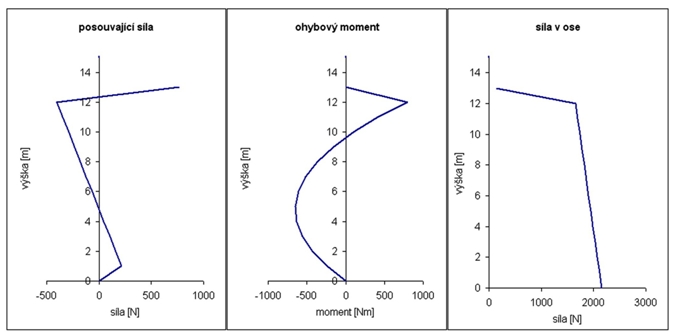
Además de su propio sistema de seguridad, también es interesante observar la distribución de algunas magnitudes a lo largo del mástil. Esto se muestra en la figura 2 (para la versión C) y 3 (E). Si la altura de arriostramiento se elige a una altura para maximizar la seguridad, entonces las formas de las curvas son muy similares - por eso muestro sólo 2 ejemplos típicos.

La base del método simple es sencilla: se agarra la cuerda en medio de dos puntos y se tira de ella lateralmente para conseguir un desplazamiento determinado. Mide la fuerza necesaria para conseguir ese desplazamiento (con una balanza de resorte, por ejemplo). Cuanto mayor sea la fuerza necesaria para conseguir el mismo desplazamiento, mayor será la tensión (lo cual es obvio).
También puedes calcular la tensión:
- Distancia entre puntos de la cuerda: L [mm]
- Desplazamiento: D [mm]
- Fuerza de tracción: F [N]
- Fuerza de tracción: T [N]
T = F * L / D / 4
La fórmula es razonablemente exacta si la distancia entre los puntos es mucho mayor que el desplazamiento (L >> D).
He aquí uno de los muchos instrumentos basados en este principio:

Hay muchas herramientas de medición diferentes en el mercado, por ejemplo de Loos&co ésta. Tenga cuidado porque estos tensores están calibrados para cuerdas de acero, no para las sintéticas. Los calibradores para cuerdas de acero suelen tener una distancia pequeña entre los puntos de medición.
Un buen indicador de la tensión en la cuerda es su comba (por supuesto, si todas las cuerdas tienen la misma longitud y no hay viento fuerte).