Martin Huml, OL5Y/OK1FUA,
En la primera parte hablamos de las fuerzas y de las cuestiones relacionadas con el arriostramiento en general; hoy hablaremos del propio mástil. Antes de empezar me gustaría agradecer todos vuestros comentarios, preguntas y demás temas. Me alegro de que os haya interesado el artículo anterior e intentaré que siga siendo así.
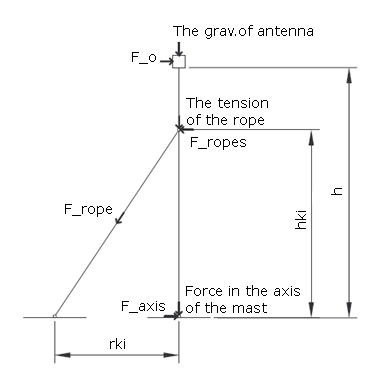
En esta secuela nos centraremos en la versión más básica: el mástil tubular atirantado en un nivel por debajo de la antena. Esta situación se ilustra en la figura 1. Para simplificar los cálculos, supondremos que todo el mástil tiene el mismo diámetro de tubo y las mismas propiedades en toda su longitud. También supondremos que la velocidad del viento a lo largo del mástil es la misma (en realidad es menor justo por encima del suelo).
Al analizar las cantidades y propiedades que afectan al comportamiento del sistema llegamos a esta lista:
- la altura total del mástil, la altura de la cuerda fijada, la distancia del ancla a la base del mástil (para determinar las fuerzas que afectan al sistema)
- diámetros exterior e interior del tubo (para determinar la resistencia y el peso del mástil)
- propiedades físicas del material del que está hecho el tubo: densidad, módulo elástico, límite de resistencia, límite proporcional (para determinar la resistencia y el peso del mástil)
- área y peso de la antena (para determinar la fuerza de resistencia al viento)
- coeficiente de resistencia del mástil y de la antena (para determinar la fuerza de resistencia al viento)
- propiedades del entorno (aire): viscosidad cinética, aceleración de la gravedad, densidad del aire
- velocidad del viento
Salidas de los cálculos que deseamos obtener:
- fuerza en el eje de la base del mástil (acción sobre el punto de colocación de la base del mástil)
- fuerza en el eje de la cuerda (para la selección de la cuerda adecuada)
Sin embargo, nos interesará especialmente la seguridad - si el mástil sobrevivirá y con qué grado de seguridad.
Pero ¿cómo evaluar y comparar la seguridad si no tiene unidad y su expresión en palabras es bastante difícil y sobre todo subjetiva? Probablemente no podremos medirla. Los sectores de la construcción utilizan una unidad llamada coeficiente de seguridad. Se calcula de forma diferente para cada tipo de estructura, pero su interpretación (sentido) es siempre la misma: Si es mayor que 1, "hay una garantía teórica de que la estructura sobrevivirá". El valor mínimo recomendado es 1,4. Si la seguridad de la estructura implica varios factores, el coeficiente se calcula para cada factor por separado y la seguridad total de la estructura es la menor de ellas. En nuestro caso, hay dos factores críticos: la resistencia del material del que está hecho el mástil (es decir, la tensión en él), y el pandeo del mástil (para que el mástil no se doble). Nuestras consideraciones darán lugar a la evaluación de la seguridad total del sistema.
De lo anterior se desprende que hay un gran número de cantidades que son diferentes para situaciones específicas. Cada uno tiene una antena diferente, un mástil diferente, una altura de mástil diferente... A modo de ilustración, he elegido varias situaciones que me parecen adecuadas para la demostración y para las que he calculado diferentes resultados. En cada caso he elegido la altura de la fijación de la cuerda para que la seguridad total sea la mayor. Las variaciones individuales son las siguientes:
- La altura del mástil de 13 m, en el que se coloca una antena ECO (3el. tribander para 10/15/20m). Esta versión está calculada para 3 mástiles diferentes: tubo de diámetro 80 mm con pared de 3 mm de espesor de un duraluminio de calidad media (ver. A), tubo del mismo material 100/4 mm (B) y tubo de acero 60/3 mm (C).
- La altura del mástil de 13 m con antena de 11el. para una banda de 2 m en dos versiones: duraluminio medio de 60 mm de diámetro con una pared de 2 mm de espesor (D) y fibra de vidrio de 60 mm de diámetro con una pared de 5 mm de espesor (E).
- La última versión es un mástil de 23 m con una voluminosa antena TH7DX (7el. tribander para 10/15/20m) de nuevo en 2 versiones: duraluminio de alta calidad de 100 mm de diámetro con una pared de 10 mm de espesor (F) y acero de 100 mm de diámetro con una pared de 5 mm de espesor (G).
Otros parámetros utilizados para los cálculos son: densidad del aire = 1,2 kg/m3, aceleración de la gravedad = 9.82 m/s2, velocidad del viento = 36 m/s = 130 km/h, coeficiente de resistencia del mástil y de la antena C = 1.2. Los resultados se muestran en el cuadro nº. 1.
| Cantidad | Símbolo | A | B | C | D | E | F | G | Unit | |
| 11m duralumin ECO | 11m duralumin ECO |
11m steel ECO |
11m duralumin 11el. 2m | 11m fibra de vidrio11el. 2m | 23m duralumin TH7DX |
23m aceroTH7DX |
||||
| mástil - tubo | ||||||||||
| altura total | h | 13 | 13 | 13 | 13 | 13 | 23 | 23 | m | |
| altura de fijación de la cuerda | h_ki | 12 | 12 | 12 | 11 | 9 | 17 | 20 | m | |
| distancia del tipo | r_ki | 10 | 10 | 10 | 10 | 10 | 15 | 15 | m | |
| diámetro exterior | D_o | 80 | 100 | 60 | 60 | 60 | 100 | 100 | mm | |
| diámetro interior | D_i | 74 | 92 | 54 | 56 | 50 | 80 | 90 | mm | |
| densidad del mástil | ro_s | 2700 | 2700 | 7850 | 2800 | 1200 | 2800 | 7850 | kg/m3 | |
| módulo elástico | E_s | 60000 | 60000 | 200000 | 60000 | 18000 | 60000 | 200000 | MPa | |
| límite de fuerza | sigma_t | 300 | 300 | 320 | 300 | 220 | 350 | 320 | MPa | |
| límite proporcional | sigma_tu | 200 | 200 | 120 | 200 | 200 | 200 | 120 | MPa | |
| reacción de la cuerda | F_ropex | 1355 | 1486 | 1223 | 629 | 768 | 2446 | 2079 | N | |
| reacción en el fondo del mástil | F_fuerzas en el eje del mástil | 2023 | 2346 | 2153 | 856 | 858 | 4951 | 5808 | N | |
| reacción en el fondo del mástil perpendicular | F_axis | -381 | -492 | -270 | -267 | -128 | -376 | -743 | N | |
| fuerza en el eje de la cuerda | F_cuerda | 2116 | 2321 | 1911 | 934 | 1034 | 3697 | 3466 | N | |
| antena | ||||||||||
| área de la antena | S_ant | 0,82 | 0,82 | 0,82 | 0,18 | 0,18 | 0,9 | 0,9 | m2 | |
| peso de la antena | m_ant | 15 | 15 | 15 | 3,5 | 3,5 | 40 | 40 | kg | |
| evaluar la seguridad | ||||||||||
| tensión en el mástil | k_t | 4,01 | 6,21 | 2,86 | 2,37 | 2,14 | 3,16 | 3,34 | ||
| pandeo | k_b | 2,47 | 5,84 | 3,62 | 2,01 | 1,89 | 3,27 | 4,75 | ||
| seguridad total | k | 2,47 | 5,84 | 2,86 | 2,01 | 1,89 | 3,16 | 3,34 | ||
En la versión (A) quería mostrar que, aunque se utiliza un tubo relativamente grueso, la seguridad total no es tan perfecta como algunos podrían esperar basándose en su experiencia. Esto se debe a que la disposición del sistema con una sola altura de tirante no es, sin duda, óptima y exige mucho al material del mástil. Hablaremos de otras versiones la próxima vez, pero puedo revelar que la resistencia del sistema en doble arriostramiento es cuatro veces mayor e incluso nueve veces mayor en niveles de arriostramiento triple (por supuesto, si se colocan en alturas óptimas). También he incluido la versión (E) porque he visto mástiles similares utilizados por varios radioaficionados.
| material | density | módulo elástico | límite de fuerza | límite proporcional |
| kg/m3 | MPa | MPa | MPa | |
| duralumin | 2800 | 60000 | 180-450 | x |
| aluminum | 2700 | 60000 | 60-150 | x |
| acero | 7850 | 200000 | 320-835 | 120-290 |
| fibra de vidrio | 1200 | 18000 | 220 | x |
Tabla nº 2: propiedades físicas de los materiales
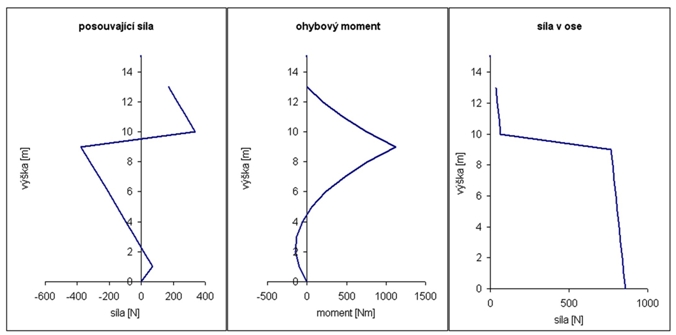
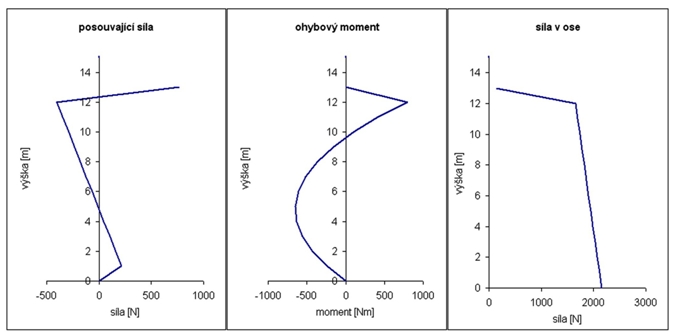
Además de su propio sistema de seguridad, también es interesante observar la distribución de algunas magnitudes a lo largo del mástil. Esto se muestra en la figura 2 (para la versión C) y 3 (E). Si la altura de arriostramiento se elige a una altura para maximizar la seguridad, entonces las formas de las curvas son muy similares - por eso muestro sólo 2 ejemplos típicos.