Tipps und Empfehlungen
Nützliche Tipps, Tricks und Ratschläge

Diese allgemeine Anleitung zeigt Ihnen, wie Sie die erforderliche Länge des Verankerungsseils effektiv einstellen, es spannen und für eine langfristige Installation sichern.
Das Verfahren eignet sich sowohl für die Installation von einfachen Masten als auch für große Antennenanlagen mit Gittermasten.
- Schrauben Sie das Spannschloss auf die maximale Länge auf.
- Befestigen Sie das Spannschloss am Anker.
- Fädeln Sie das Seil durch die obere Öse/Kausche.
- Bringen Sie die Schlaufenspannvorrichtung an ihrem freien Ende an. Verwenden Sie CL234 für Seile 6 bis 11 mm (1/4" bis 1/2") oder CL223 für Seile 3 bis 6 mm (1/8" bis 1/4").
- Stellen Sie die gewünschte Länge des Ankerseils ein oder passen Sie die Länge schrittweise an. Vorteilhaft ist die Verwendung eines Klampen-Spanners, der sich leicht auf dem Seil verschieben lässt. Das Verfahren unterscheidet sich je nach der Art der Installation des Mastes/Turms und der Abspannseile (Anheben des zusammengeklappten Mastes vom Boden, schrittweises Ausfahren des Teleskopmastes, Installation des Mastes in Teilen, ...).
- In der Arbeitsposition (vor dem endgültigen Spannen) sollte das Spannelement etwa so aussehen:


- Spannen Sie das Seil nach der Einstellung mit einem Stollenspanner.
- Bringen Sie die Seilklemme an und ziehen Sie sie fest an:


- Jetzt können Sie den Klampen-Spanner lösen und mindestens 2 Sicherheitsknoten (Double Half-hitch) machen:

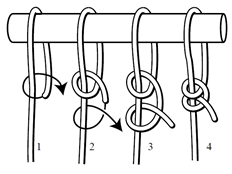
- Ziehen Sie die Knoten fest an und sichern Sie das freie Ende des des Seils mit Kabelband (für Seile bis ca. 5 mm - 3/16 ") Seile oder bringen Sie eine zweite Sicherungsklemme an.
- Spannen Sie das Abspannseil mit Hilfe eines Spannschlosses auf die erforderliche Spannung:


- Ziehen Sie die Seilklemmen fest an. Wenn Sie Spanner mit Kontermuttern verwenden (wie die Wantenspanner (Gabel-Gabel) auf dem Bild), ziehen Sie diese Muttern ebenfalls fest.
- Bevor Sie beginnen, lesen Sie bitte unsere Artikel Grundlegende Richtlinien zur Verankerung mit synthetischen Seilen und Montageanleitung für Halteseile.

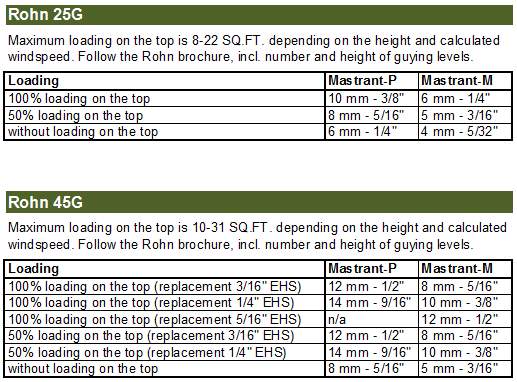
Empfohlener Ersatz von Stahlseilen durch Mastrant-Synthetikseile - nur auf Basis der Festigkeit!
| Stahl (1570 Mpa) | P | M |
| 4 mm (5/32") | 6 | 4 |
| 5 mm (3/16") | 8 | 5 |
| 6 mm (1/4") | 10 | 6 |
| 7 mm (9/32") | 12 | 8 |
| 8 mm (5/16") | 14 | 10 |
| 9 mm (11/32") | - | 12 |
| 10 mm (3/8") | - | 12 |
| Verzinkte EHS | P | M |
| 5 mm (3/16") 1x7 | 10 | 6 |
| 6 mm (1/4") 1x7 | 14 | 8/10 |
| 8 mm (5/16") 1x7 | - | 12 |

Beim Entwurf eines „Verankerungssystems“ (Verankerungsseil mit Endstücken, Kupplungen und Seilklemmen) müssen folgende Faktoren in Betracht gezogen werden:
- Die Stabilität des Systems hängt von der Stabilität seines schwächsten Gliedes ab. Aus diesem Grund ist es nicht effektiv, ein 50kN starkes Seil mit einem Spannhalter von 5kN zu verwenden.
- Sogar das beste synthetische Seil ist elastisch – beim Abspannen dehnt es sich aus. Bei der Planung des Masts und seiner Verankerung (ebenso bei der Befestigung der Antennenteile), muss man diese Eigenschaft in Betracht ziehen und stets berücksichtigen, wie die Dehnung des Verankerungssystems die gesamte Konstruktion beeinflusst. In Einzelfällen muss ein stärkeres Seil benutzt werden (mit geringerer absoluter Dehnbarkeit), im Gegensatz zu Konstruktionen, die durch eine Verlängerung der Verankerung nicht negativ beeinträchtigt werden. Probleme entstehen vor allem dann, wenn sich der Bodenverankerungspunkt zu nah an der Mastbasis befindet bzw. unter Einsatz eines Gittermasts mit geringer Flexibilität.
- Das Seil muss außer Reichweite von scharfen Kanten sein. Es muss also mit einer Kausche befestigt oder an eine Kupplung mit sehr glatter Oberfläche gebunden werden. Achtung: Ungeeignete Metallmaterialien können korrodieren und ihre Oberfläche raut auf. Sie sollten niemals Seile an Betonsäulen oder Steinelement festbinden! Wenn Sie Stein, Fels oder eine Betonsäule als Bodenverankerungspunkt verwenden wollen, empfehlen wir den Einsatz einer Stahlseilschlaufe, die mithilfe einer glatten Kupplung am Abspannseil befestigt werden kann.
- Die größte Gefahr für Seile besteht bei Reibung mit Objekten, die sich in seiner Bahn befinden (z.B. Äste, Steine, Gebäudeteile...). Sogar abgespannte Seile bewegen sich im Wind, was zur Abnutzung des Seils führen kann. Besonders gefährlich ist Reibung an Ästen (Seil–Ast–Reibung). Diese bewegen sich unter Windeinfluss oft relativ stark und wenn das Seil an Ästen scheuert, ist die Wahrscheinlichkeit ernsthafter Beschädigung innerhalb weniger Tage extrem hoch. Wenn Sie Bäume zur Befestigung von Antennen benutzten, empfehlen wir den Einsatz von Stahlseilen in Biegepositionen über Ästen und die Verankerung des Stahlseils mithilfe von Seilrollen.
- Der untere Teil des Verankerungssystems sollte aus 2–4 m langen Stahlseilen bestehen um sicher zu stellen, dass das synthetische Seil nicht von Tieren „angeknabbert“ oder (absichtlich oder unabsichtlich) von Menschen beschädigt wird.
Der Abschluss des Seils ist eines der wichtigsten Sicherheitselemente.
- Abspannseile können am Ende mit einer Kausche zur dauer-haften Abspannung versehen werden. Oder sie werden direkt am Objekt angebunden.

- Wenn das Seil am Objekt angebunden wird, sollte sichergestellt sein, dass sich das Seil nicht bewegt oder scheuert. Besser ist es natürlich wenn das Seil zuerst an einem Schäkel oder Karabinerhaken befestigt wird. Und dieser wird dann im Befestigungspunkt des Mastes eingehängt.

- Auf jede Kausche muss natürlich eine Seilklemme folgen. Wir empfehlen Duplex-Seilklemmen oder einfache Seilklemmen mit Pressbacken. Hinter der Seilklemme sollte natürlich das offene Ende des Seiles durch ein weiteres Sicherungselement befestigt werden. Entweder durch eine weitere Klemme oder durch eine sogenannte Ankerbindung. Zu guter letzt sollte das offene Ende gegen Aufdrehen mit einem Kabelbinder gesichert werden.


- Andere Möglichkeit ist die Verwendung von Crimp-Terminals. Das ist nur an einem Ende des Seils praktisch - ansonsten ist es nicht möglich, die Länge einzustellen. Wir verkaufen sie als "Seil mit Kausche" - hier.

- Abgespannte Seile verändern unter Last ihren Durchmesser, sie werden dünner. Deswegen sollten alle Klemmen nach einiger Zeit nachgezogen werden.
- Vorsicht vor den klassischen „bull-dog grips“. Diese Seilklemmen sind speziell für Stahlseile entwickelt worden. Wenn sie zu stark angezogen werden, können Sie das Kunststoffseil abschneiden. Wir empfehlen Ihnen unter keinen Umständen diese Seilklemmen als erste Klemme zu verwenden. Lediglich als zweite Sicher-heitsklemme könnten sie verwendet werden.
- Wir würden vorschlagen spezielle Abspannhalter zu verwenden. Leider sind sie relativ teuer. Aber sie bieten viele Vorteile und schonen das Seil. Durch spezielle Klemmbacken halten Sie das Seil, auch wenn es unter Zug dünner wird. Außerdem ist ein Nachspannen ohne weiteres möglich.

Häufig gemachte Fehler durch die Unfälle entste-hen:
- Der Abspannpunkt ist zu nahe am Mast und dadurch ist der Abspannwinkel kleiner 45°.
- Die Seilklemmen wurden nach dem Aufstellen des Mastes nicht nachgezogen!
- Hinter den Seilklemmen wurde keine zweite Klemme zur Sicherheit angebracht.
- Es wurde keine Seilkausche verwendet sondern das Seil wurde direkt am Mast angebunden.
- Das Seil wurde durch ein Tier oder einen Menschen beschädigt (angeknabbert, bzw. durchgeschnitten).
- Verwendung eines ungeeigneten Seil mit hoher Dehnung.


- Berechnen oder messe sie die benötigte Länge der Abspannseile.
- Addieren sie dazu die Länge welche für eine sichere Befestigung (Seilkausche, Seilklemme, Knoten) benö-tigt wird. Die Länge ist ungefähr der 60-fache Durchmesser des Seiles.
- Schneiden sie das benötigte Seil mit einem heißen Messer ab. Alternativ kann das Seil auch mit einem scharfen Messer abgeschnitten werden. Nach dem Schneiden muss das Ende auf jeden Fall mit einer Flamme oder einem heißen Lötkolben verschmolzen werden. Der Kunststoff schmilzt bei 150°C (Dyneema) bis 260°C (Polyester).
- Legen sie die Seilkausche bereit. Sollte es notwendig sein, kann die Seilkausche mit einer Zange etwas auf-gebogen werden um sie über den Haltepunkt zu bekommen. Sie sollte dann aber auch wieder zugebo-gen werden. Kleine Unebenheiten oder Fehlstellungen (nach dem Zubiegen) haben keinen Einfluss auf die Zugfestigkeit.
- Legen sie die Seilklemme bereit und zerlegen sie wie auf dem Bild zu sehen.
- Legen sie das Seil um die Seilkausche und in die Seil-klemme (wie im Bild zu sehen). Dann schrauben sie die Seilklemme wieder zusammen. Das offene Ende des Seiles muss jetzt noch eine Länge von dem 35-fachen des Seiles haben (für die Sicherheitsknoten).

- Befestigen sie die Seilklemme so nah als möglich an der Seilkausche.
- Jetzt sind die Schrauben der Seilklemme anzuziehen. Mit Gefühl!!!!! Nun sind mit dem restlichen Seilende zwei Knoten zu machen. Das Seilende ist mit einem Kabelbinder zu sichern.

- Bedingt durch die Spannung des Seiles ist es notwen-dig die Seilklemmen immer wieder nachzuziehen (Seil wird unter Spannung dünner!).Sollten Sie den Ab-spannpunkt nach dem Aufbau des Mastes nicht mehr erreichen, dann müssen Sie die Muttern vorher schon kräftig anziehen.
- Bringen sie das Seil an der geplanten Stelle an und ziehen sie die Schrauben der Seilklemme vorsichtig etwas an.
- Überprüfe sie ob das Seil in den Seilklemmen ge-rutscht ist. Wenn dem so ist, muss das Seil nachgespannt werden.
- Ein Vorteil ist, wenn an den Abspannpunkten Seil-spannschlösser eingesetzt werden. Ausfahrbare Masten können auch ohne Seilspannschlösser abge-spannt werden. In diesem Fall sollten die Seile schon gespannt werden, wenn der Mast noch nicht ganz ausgefahren ist. Erst dann ist der Mast ganz auszufah-ren. Diese Prozedur ist aber von Mast zu Mast unterschiedlich.
- Die optimale Vorspannung der Seile hängt von ver-schiedenen Faktoren ab: Die Art des Mastes, Typ und Dicke des Seiles, Abstand zwischen Abspannpunkt und Maststandort. In den meisten Anwendungen sollte die benötigte Haltekraft des Seiles bei 5-20% der Fes-tigkeit des Seiles betragen. Und nicht vergessen!! Bitte für jeden Mast extra berechnen!
- Nachdem der Mast steht und die Seile auch richtig gespannt sind, sollte man auf jeden Fall die Spannung der Seite am nächsten Tag und dann im Abstand von einer Woche für einige Wochen kontrollieren.
Häufig gemachte Fehler durch die Unfälle entste-hen:
- Der Abspannpunkt ist zu nahe am Mast und dadurch ist der Abspannwinkel kleiner 45°.
- Die Seilklemmen wurden nach dem Aufstellen des Mastes nicht nachgezogen!
- Hinter den Seilklemmen wurde keine zweite Klemme zur Sicherheit angebracht.
- Es wurde keine Seilkausche verwendet sondern das Seil wurde direkt am Mast angebunden.
- Das Seil wurde durch ein Tier oder einen Menschen beschädigt (angeknabbert, bzw. durchgeschnitten).
Martin Huml, OL5Y/OK1FUA,
(Hinweis: alle Tabellen sind im Excel-Format verfügbar)
Während meiner Amateurfunkaktivitäten widme ich (wahrscheinlich wie jeder von uns) die meiste Zeit der Frage der Antennen. Und eine der wichtigsten und vielleicht auch schwierigsten Aufgaben ist es, die Antenne "in die Luft" zu bekommen und sie dort zu halten. Offenbar gilt das für alle Antennen, vielleicht mit Ausnahme von Getränkeantennen... Ich habe über dieses Thema in dem Artikel "Wie man einfache Antennenmasten baut und abspannt" (Zeitschrift "Radioamatér" 2 & 3/2004) geschrieben. Schon damals hatte ich das Gefühl, dass dieses Thema so interessant, kompliziert und umfangreich ist, dass es angebracht wäre, darauf zurückzukommen.
Ein weiteres Motiv, den folgenden Artikel zu schreiben, war, die Fragen einzubeziehen, die entweder von meinen Freunden gestellt wurden oder von selbst auftauchten, z.B. "Warum machst du die Vertikale so tief?", "Wird dieses Seil stark genug sein?", "Wird dieser Mast die Antenne tragen können?" und so weiter. Meistens konnte ich keine bessere Antwort finden als "weil ich denke, dass es ausreicht" oder "weil ich es irgendwo so gesehen habe". Das klingt nicht sehr wissenschaftlich. Praxis und Erfahrung sind großartig und unersetzlich, aber zu viel davon ist reine Spekulation, und so beschloss ich, als meine Aktivitäten mich zum "Guying" führten, es auch aus theoretischer Sicht zu betrachten. Zunächst möchte ich betonen, dass ich kein Ingenieur bin; daher habe ich mich nach einiger Zeit des Studiums an den Ingenieur Richard Beber gewandt, der sich im Gegensatz zu mir mit diesem Thema beschäftigt hat. An dieser Stelle möchte ich ihm danken - ohne ihn wäre der Artikel nicht geschrieben worden.
Wie der Name dieses Artikels schon andeutet, geht es in erster Linie darum, wie man Antennen abspannt. Das bedeutet aber nicht, dass Besitzer von freistehenden Masten nicht auch etwas Interessantes finden. Zum Beispiel könnten Berechnungen der Kräfte, die bei Wind auf die Antenne wirken, oder andere Dinge nützlich sein.
Verwendete Begriffe und Vereinfachung
Ich bitte die Experten und Sprachwissenschaftler um Nachsicht - ich verwende diese Begriffe so, wie ich sie aus der Amateurpraxis kenne:
- Montageort = die Stelle, an der das Abspannseil am Mast montiert (befestigt) ist
- Montagehöhe = der Abstand zwischen dem Montagepunkt und dem Mastfuß (HKI)
- Abspannpunkt = die Stelle, an der das Abspannseil am Boden (oder einem anderen festen Punkt) befestigt ist
- Abspannabstand = der Abstand zwischen dem Abspannpunkt und dem Mastfuß (Sockel, beschriftet mit RKI)
- Das System = der Mast mit Antenne
Eine Vertikalantenne ist eigentlich ein Mast ohne Antenne. Daher werde ich im folgenden Text nicht zwischen diesen beiden Antennentypen unterscheiden, wo es nicht angebracht ist. Mit anderen Worten: Die Formulierung "Abspannung in der Mitte des Mastes" ist als "Abspannung in der Mitte der Vertikalen" zu verstehen.
Wenn nicht anders angegeben, gehen wir davon aus, dass der Mast auf einer horizontalen Fläche steht; daher befinden sich die Bodenabspannungen und der Mastfuß auf der gleichen Ebene, senkrecht zur Mastachse. Dies dient der Vereinfachung - die Realität sieht sicherlich anders aus. Deshalb wird im folgenden Text aufgezeigt, wie man mit der Realität umgehen kann.
In unseren Überlegungen gehen wir auch nicht auf das Verhalten der Antenne selbst ein - wir gehen davon aus, dass sich die Antenne am Mast nicht verändert.
Und schließlich, für diejenigen, die keine Freunde der Physik sind - wir werden viel über Kraft sprechen, deren Einheit 1 N (Newton) ist. Wenn Sie zum Beispiel ein Gewicht von 1 kg heben, beträgt die auf Sie wirkende Kraft etwa 10 N.
Die Antenne und der Mast
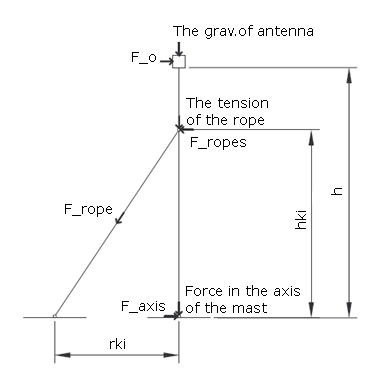
Betrachtet man das vereinfachte Modell des Abspannmastes und der Antenne an seiner Spitze (Abb. 1), so wirken folgende Kräfte auf das System:
- Schwerkraft (Masse des Mastes, der Seile und der Antennen),
- widerstandsfähige Windkraft,
- Spannungskraft der Abspannseile.
Diese Kräfte erzeugen eine Reaktion, so dass die resultierenden Kräfte ausgeglichen werden. Die Reaktion zeigt sich in der Einspannung des Mastbodens und an den Befestigungsstellen der Abspannseile. Außerdem kommt es zu einer flexiblen Verformung des Mastes und der Seile. Wir betrachten hier nicht die irreversible Verformung oder Zerstörung des Materials - diese Fälle wollen wir vermeiden und konzentrieren uns daher auf die Ermittlung aller wirkenden Kräfte.
Die Kräfte stellen jedoch nicht alle Faktoren dar, die das Verhalten des Systems beeinflussen werden. Wir dürfen die Struktur des Mastes (Rohr, Gitterstruktur usw.) und das Material, aus dem er besteht, nicht vergessen, insbesondere seine physikalischen Eigenschaften wie Dichte (spezifisches Gewicht), Flexibilität und Festigkeit. Ebenso müssen wir die Eigenschaften der Abspannseile kennen - ihre Festigkeit und Dehnung. Fassen wir also zusammen, was wir wissen müssen:
- Antenne - Masse
- Antenne - Form (Anzahl, Länge und Durchmesser der Elemente)
- Mast - Struktur, Material
- Abspannseil - Dehnung (Dehnung bei Arbeitslast), Festigkeit
Die Parameter, mit denen wir uns beschäftigen werden, sind folgende
- Gesamthöhe (die Höhe der Antenne über dem Boden = die Höhe des Mastes)
- die Anzahl der Abspannrichtungen (3 oder 4)
- die Anzahl der Abspannungsebenen (auf wie vielen Ebenen wird der Mast abgespannt)
- die Höhe der Abspannseilbefestigung(en)
- der Abstand des Abspannpunktes vom Fußpunkt
Der Abstand der Abspannung
Die erste Frage, mit der wir uns beschäftigen werden, ist der Einfluss des Abspannabstandes auf die Größe der Kräfte (die auf den Mast und die Abspannseile wirken). Wir werden diese Aufgabe in folgende Randsituationen unterteilen: Im ersten Fall weht der Wind aus der Richtung der Abspannung, im zweiten Fall weht der Wind "zwischen den Abspannungen". (Abb. 2)
Wenn der Wind aus der Abspannrichtung weht, handelt es sich um eine einfache Zusammensetzung von Kräften - der Fall eines rechtwinkligen Dreiecks, bei dem einer der Schenkel der Mast (h) ist, der zweite der Abstand zwischen dem Mastfuß und dem Abspannpunkt (r), wobei das Abspannseil die Hypotenuse (l) ist. Das Verhältnis, in dem die einzelnen Schenkel dieses Dreiecks stehen, ist das Verhältnis der Kräfte, die in die einzelnen Richtungen wirken. Wir kennen (können berechnen) die Kraft Fant, die durch den Wind auf die Antenne wirkt. (Ihr spezifischer Wert ist in diesem Moment nicht wichtig; wir werden uns später damit befassen - da wir jetzt den Einfluss der Entfernung des Abspannpunkts beurteilen). Die auf den Mast (in seiner Achse) wirkende Kraft ist also Fst = Fant * h / r, und die auf das Abspannseil wirkende Kraft ist Fko = Fant * l / r. Wir berechnen die Länge des Seils mit dem Satz des Pythagoras: l = √(h2 + r2).
Wenn der Wind aus der Richtung der Achse zwischen den Abspannungen weht, ist die Situation etwas komplizierter, weil wir den Winkel zwischen den Abspannungen berücksichtigen müssen - mit anderen Worten, in wie viele Richtungen der Mast abgespannt ist.
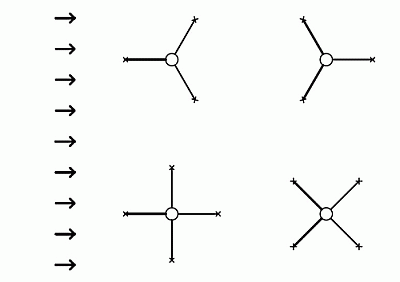
Abspannrichtungen
Zu diesem Zweck betrachten wir den Mast von oben und führen insgesamt 3 Punkte ein - den Mast und 2 Abspannpunkte. Weiterhin führen wir die Richtung ein, aus der der Wind weht - es ist die Achse zwischen den Abspannpunkten, die durch den Mast geht. Die Stelle, an der diese Achse die Verbindungslinie zwischen unseren beiden Abspannpunkten schneidet, ist ein Punkt, der den virtuellen Abspannpunkt für die Berechnung der wirkenden Kräfte darstellt. Wir sehen, dass er viel näher am Mastfuß liegt als der Abspannabstand - je näher er liegt, desto größer ist der Winkel zwischen den Abspannungen.
Auch hier handelt es sich um Dreiecke, aber nicht unbedingt um rechtwinklige Dreiecke. Wenn wir die grundlegenden goniometrischen Funktionen anwenden, kommen wir zu diesen Beziehungen:
Für 4 Stäbe in 90°:
Fst = Fant * (h / r) * √2 = Fst = Fant * (h / r) * 1,414
Fko = Fant * (l / r) * (√2) / 2 = Fant * (l / )r * 0,707
für 3 Abspannungen von je 120°:
Fst = Fant * (h / r) / cos(60/180π) = Fant * (h / r) / 0,5
Fko = Fant * (l / r) / cos(60/180π) = Fant * (l / )r .
Auf den ersten Blick wird vielleicht eine interessante Eigenschaft übersehen - bei Abspannung in 3 Richtungen ist die auf das Abspannseil wirkende Kraft die gleiche wie bei Wind "von der Abspannung" und "zwischen den Abspannungen".
Wie sieht das in der Praxis aus?
Von der theoretischen Perspektive, die für die meisten von uns wahrscheinlich langweilig ist, kommen wir nun zu den praktischen Auswirkungen. (Ich verspreche, dass der folgende Text ohne Formeln auskommt - sie wären viel komplizierter ...)
Zur Veranschaulichung habe ich ein einfaches Beispiel gewählt - einen 10 m hohen Mast mit einem Dreifuß (10/15/20 m) an der Spitze. Ich wiederhole noch einmal - es ist ein Beispiel, um die Auswirkungen des Abspannabstands und der Anzahl der Richtungen, in die der Mast abgespannt ist, zu zeigen.
Daher sind wir nicht an den Eigenschaften des Mastes oder des Seils interessiert. Wir lassen also den Wind mit 130 km/h auf den Tribander blasen. Es lässt sich annähernd berechnen, dass die wirkende Windkraft etwa 775N beträgt. Wie ich zu diesem Ergebnis gekommen bin, werde ich im nächsten Kapitel erläutern; für den Moment reicht dieses Ergebnis aus.
Ich möchte jedoch eine sehr wichtige Tatsache erwähnen, nämlich dass die Kraft proportional zum Quadrat der Geschwindigkeit ist (z.B. halbe Geschwindigkeit = viertel Kraft; die Kraft im Falle von 80 km/h beträgt also ca. 290 N). Allerdings wächst die Kraft in ähnlichem Maße - Sie können also nachvollziehen, was ein Tornado mit einer Windgeschwindigkeit von über 300 km/h in seinem Zentrum anrichten kann, denken Sie also bitte nicht, dass fliegende Autos eine reine Erfindung der amerikanischen Filmemacher sind.
Aber nun zurück zu den Abspannungen. In den folgenden Tabellen sehen Sie die berechneten Kräfte für beide Varianten der Abspannung (3 und 4 Richtungen) und für die Abspannung von 10 und 5 m. Ich denke, es ist offensichtlich, dass eine Annäherung der Abspannpunkte an den Mast zu einer unnötigen Erhöhung der wirkenden Kräfte führt. Ähnlich verhält es sich bei der Abspannung in 3 Richtungen, die die Belastung des Mastes erhöht.
| Höhe der Fixierung | 10 m | ||
| Abstand der Abspannpunkte | 10 m | ||
| Geschwindigkeit des Windes | 130 km/h | ||
| Richtung des Windes | Anzahl der Richtungen | Kraft [N], die wirkt: | |
| Abspanndraht | Mast | ||
| aus Richtung des Abspannseils | 4 | 1 095 | 775 |
| zwischen dem Abspannseil | 4 | 775 | 1 095 |
| aus Richtung des Abspannseils | 3 | 1 095 | 775 |
| zwischen dem Abspannseil | 3 | 1 095 | 1 245 |
| Höhe der Fixierung | 10 m | ||
| Abstand der Abspannpunkte | 5 m | ||
| Geschwindigkeit des Windes | 130 km/h | ||
| Richtung des Windes | Anzahl der Richtungen | Kraft [N], die wirkt: | |
| Abspanndraht | Mast | ||
| aus Richtung des Abspannseils | 4 | 1 732 | 1 549 |
| zwischen dem Abspannseil | 4 | 1 224 | 2 191 |
| aus Richtung des Abspannseils | 3 | 1 732 | 1 549 |
| zwischen dem Abspannseil | 3 | 1 732 | 3 098 |
Wie Sie sehen können, sind die Kräfte, die durch solch starken Wind verursacht werden, bei einer vernünftigen Auslegung nicht so groß. Mit anderen Worten - wir brauchen keine extremen Seile, um eine solche Antenne abzuspannen. Wie an vielen Stellen zu sehen ist, hält auch ein relativ schwaches Seil, wenn es für diesen Zweck vorgesehen ist. Die schwächsten Stellen sind alle Gelenke ... Und unter unseren Bedingungen dürfen wir die Situationen nicht vergessen, in denen die Antenne von Frost umhüllt ist ... Aber das ist wirklich eine Ablenkung und wir werden darauf zurückkommen.
Nur zum Abschluss noch ein Absatz - aufmerksame Leser haben sicher bemerkt, dass es nicht um die absolute Höhe und den Abstand geht - wir erhalten die gleichen Ergebnisse mit einem Mast von 20m und dem Abstand von 20 und 10m. Es geht um den Winkel, der zwischen dem Abspannseil und dem Mast gebildet wird. Dies sollte vor allem in Situationen berücksichtigt werden, in denen der Abspannpunkt nicht in einer Ebene senkrecht zum Mast platziert werden kann (er befindet sich an einem Hang). Wenn man in einem solchen Fall z.B. den Abspannpunkt 3m tiefer als den Mastfuß setzen muss und den Winkel zwischen Seil und Mast 45° beibehalten will, muss man den Abspannpunkt 13m von der Mastachse (Vorsicht, nicht vom Mastfuß!) setzen. Dies ist manchmal schwer zu berechnen, deshalb kann man die Länge des Abspannseils berechnen und messen - in diesem Fall 13*1,41 = 18,3m (1,41 = √2).
Windkraft
Wenn wir einen Gegenstand in den Flüssigkeitsstrom, in unserem Fall die Luft, bringen, wird er durch die Reibungs- und Druckelemente einen Widerstand verursachen. Dieser Widerstand wird in aerodynamischen Windkanälen experimentell bestimmt und in Bezug auf die Widerstandskraft ausgedrückt:
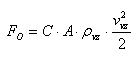 ,
,
wobei FO die Widerstandskraft [N], C der Widerstandskoeffizient des Objekts (-), A die Fläche des Objekts senkrecht zur Windrichtung [m2], ρvz die Luftdichte [kg/m3], &vvz die Windgeschwindigkeit [m/s] ist.
Der Wert des Widerstandskoeffizienten ist nicht konstant, sondern hängt von der so genannten Reynoldschen Zahl ab - einem dimensionslosen Kriterium, das das Verhältnis von Trägheit und Viskosität ausdrückt
Re = vvz * d / v ,
wobei d die charakteristische Abmessung [m] und v die kinematische Viskosität der Luft ist.
Vereinfacht man die Antenne (in unserem Fall ein Tribander) zu mehreren Zylindern, so ist die charakteristische Abmessung der Durchmesser und Re ist unter normalen Bedingungen etwa 104, während der Widerstandskoeffizient des Objekts C etwa 1,2 beträgt. Durch die auf die Antenne wirkende Widerstandskraft (Rohrdurchmesser d = 35 mm, Länge l = 23,6 m, Windgeschwindigkeit vvz = 36 m/s = 130 km/h; Luftdichte 1,2 kg/m3) können wir bestimmen:
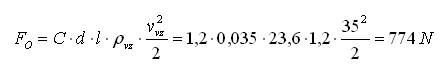 .
.
Diese Kraft wirkt als kontinuierliche Belastung auf die gesamte Antenne (wenn wir die tatsächliche Situation auf das gleiche Geschwindigkeitsprofil für die gesamte Oberfläche der Antenne vereinfachen). Wir können die auf den Mast wirkende Widerstandskraft auf ähnliche Weise bestimmen.
Die folgende Tabelle zeigt die Kräfte, die für verschiedene typische Antennen berechnet wurden (ich entschuldige mich bei denjenigen, die ihre genaue Antenne nicht in der Tabelle finden können, bitte einfach extrapolieren).
| Antenne | Windbereich [m2] | Kraft des Windes [N] bei einer Geschwindigkeit von [km/h] | ||
| 50 | 130 | 180 | ||
| HF - 3el. Tribander ECO | 0,82 | 116 | 765 | 1476 |
| HF - 3el. Tribander A3S | 0,40 | 56 | 373 | 720 |
| HF - 3el. Tribander TH3JRS | 0,32 | 45 | 299 | 576 |
| HF - 7el. Tribander TH7DX | 0,88 | 124 | 821 | 1584 |
| HF - 11el. 5-Band TH11DX | 1,17 | 165 | 1092 | 2106 |
| HF - 10el. LP 10-30m LP1010 | 1,49 | 210 | 1390 | 2682 |
| HF - 5el. für 6m F9FT | 0,13 | 18 | 121 | 234 |
| HF - 5el. für 10m LJ105CA | 0,37 | 52 | 345 | 666 |
| HF - 5el. für 15m LJ155CA | 0,49 | 69 | 457 | 882 |
| HF - 5el. für 20m LJ205CA | 0,84 | 119 | 784 | 1512 |
| HF - 6el. für 20m HD OWA | 1,80 | 254 | 1680 | 3240 |
| HF - vertikal 6-20m R6000 | 0,14 | 20 | 131 | 252 |
| HF - vertikal 6-40m R8 | 0,24 | 34 | 224 | 432 |
| HF - Inv.V Vollformat 20-160m | 0,90 | 127 | 840 | 1620 |
| 2m - 9el. 2M9 | 0,12 | 17 | 112 | 216 |
| 2m - 11el. F9FT | 0,18 | 25 | 168 | 324 |
| 2m - 12el. 2M12 | 0,14 | 20 | 131 | 252 |
| 2m - 17el. F9FT | 0,29 | 41 | 271 | 522 |
| 2m - 18el. 2M18XXX | 0,30 | 42 | 280 | 540 |
| 70cm - 18el. 440-18 | 0,08 | 11 | 75 | 144 |
| 70cm - 21el. 440-21ATV | 0,12 | 17 | 112 | 216 |
| 70cm - 38el. 432-13WLA | 0,24 | 34 | 224 | 432 |
| 23cm - 35el. 23CM35EZ | 0,06 | 8 | 56 | 108 |
Was kann durch Frost verursacht werden?
Der Frost, der ein sehr wichtiges Element in unseren Berechnungen ist und die Funktion (sowie das Überleben) der Antenne beeinträchtigt, verursacht
- Erhöhung der Oberfläche, der Windeffekte und
- Massezunahme.
Da ich keine persönlichen Erfahrungen mit Frost habe, habe ich mich zu diesem Thema mit einigen Freunden beraten, die ihre Antennen an verschiedenen problematischen Orten stehen haben, auch an solchen, wo der Frost mehrere Monate dauert. Ihre Erfahrung zeigt, dass der Frost auf den Bauteilen den ursprünglichen Durchmesser um 50 bis 100 % und in extremen Fällen um bis zu 200 % vergrößert (das Bauteil vergrößert dann seinen Durchmesser). Schauen wir uns an, wie sehr dies die Windlast erhöht.
Das vorangegangene Kapitel hat gezeigt, dass die Widerstandskraft des Windes direkt proportional zur Fläche der Antenne senkrecht zur Windrichtung und damit zum Durchmesser ihrer Komponenten ist. Wenn also der Durchmesser der Komponenten um das Doppelte zunimmt, verdoppelt sich die Windkraft. Dies sind sehr einfache Berechnungen - wenn Sie eine Antennenanlage für extremen Frost entwerfen wollen, multiplizieren Sie die Kräfte mit 3.
Die Frage der Masse ist komplizierter. Um sie zu berechnen, müssen wir nicht nur die Dicke des Frostes, sondern auch seine Dichte kennen. Obwohl die Dichte von Eis 917 kg/m3 beträgt, wird die in der Literatur und in Normen angegebene Dichte von Frost mit 400-500 kg/m3 angegeben - rechnen wir lieber mit 500 kg/m3. Da wir uns für die Zunahme der Masse der stehenden Antenne interessieren, müssen wir auch die Dichte des Materials kennen, aus dem sie hergestellt ist. In der Regel handelt es sich um eine Aluminiumlegierung mit einer Dichte von etwa 2800 kg/m3.
Eine kurze Anmerkung zur Berechnung: Der Einfachheit halber betrachten wir wieder eine Antenne, die aus Rohren oder Stäben besteht. Die Masse des Objekts m = V * ρ, wobei V das Volumen und ρ die Dichte ist. Das Volumen des Zylinders ist V = π * r2 * l, wobei r der Radius und l die Länge ist. Wenn wir die bekannten Werte einsetzen, können wir die ursprüngliche Masse und die Masse des Frosts berechnen. Dies wird im Folgenden demonstriert.
| Gestaltung des Elements /Ausleger | Multiplikation des Gewichts mit Vereisung: | ||
| 50% | 100% | 200% | |
| Sparren (alle Durchmesser) | 1,2 | 1,5 | 2,4 |
| Rohr ø 8 mm, Wandung 1 mm | 1,5 | 2,2 | 4,3 |
| Rohr ø 10 mm, Wandung 1 mm | 1,6 | 2,5 | 5,0 |
| Rohr ø 14 mm, Wandung 1 mm | 1,8 | 3,0 | 6,4 |
| Rohr ø 24 mm, Wandung 1 mm | 2,4 | 4,4 | 9,9 |
| Rohr ø 24 mm, Wandung 2 mm | 1,7 | 2,8 | 5,7 |
| Rohr ø 30 mm, Wandung 1 mm | 2,7 | 5,2 | 12,1 |
| Rohr ø 30 mm, Wandung 2 mm | 1,9 | 3,2 | 6,7 |
| Rohr ø 50 mm, Wandung 1 mm | 3,8 | 7,8 | 19,2 |
| Rohr ø 50 mm, Wandung 2 mm | 2,5 | 4,5 | 10,3 |
Die in der Tabelle dargestellten Fakten mögen für einige Leute schockierend sein. Es ist nicht leicht zuzugeben, dass eine Antenne, die z. B. aus Rohren mit 24 mm Durchmesser und 1 mm Wand besteht, ihre Masse bei 100%igem Frost um das 4,4-fache erhöht! Andererseits muss man bedenken, dass die Bedingungen für eine kontinuierliche Frostbildung auf dem gesamten Umfang der Röhre, insbesondere bei Röhren mit größeren Durchmessern, in gewöhnlichen QTHs relativ selten sind.
Interessanterweise sagt Wikipedia Folgendes über Frost aus:
Der Reif ist ein atmosphärisches Phänomen, das durch die Bildung von Eiskristallen auf der Oberfläche eines Objekts durch folgende Effekte entsteht:
• Gefrieren winziger Tröpfchen der Luftfeuchtigkeit (Wolken, Nebel usw.) bei Kontakt mit der Oberfläche des Bodens, eines Objekts oder anderer Gegenstände mit einer Temperatur von 0 °C und darunter;
• Niederschlag (Sublimation) von Luftfeuchtigkeit auf einer ausreichend kalten Oberfläche des Bodens oder von Gegenständen, und zwar auch ohne Vorhandensein von Nebel oder Wolken.
Die höchste Wahrscheinlichkeit der Frostbildung besteht bei einer Temperatur (0 bis -4 °C) beim Kontakt zwischen der Oberfläche des Objekts und dem feuchten Luftstrom. Bei Temperaturen unter -4 °C nimmt die Möglichkeit der Frostbildung ab, und bei Temperaturen unter -12 °C tritt kein oder nur sehr schwacher Frost auf.
Die obigen Daten sind vor allem bei der Betrachtung der Struktur & und des Designs der Antenne interessant - inwieweit sollten die Komponenten und der Boom dimensioniert und verstärkt werden, um ein Verbiegen zu vermeiden. Das ist wiederum ein ganz anderes Thema.
Nächstes Mal werden wir uns auf die Abspannung eines echten Mastes konzentrieren, einschließlich Überlegungen zu seiner Festigkeit und anderen beeinflussenden Elementen.

Martin Huml, OL5Y/OK1FUA,
Im ersten Teil haben wir über die Kräfte und die Probleme bei der Abspannung im Allgemeinen gesprochen; heute werden wir über den Mast selbst sprechen. Bevor ich beginne, möchte ich mich für all Ihr Feedback, Ihre Fragen und sonstigen Themen bedanken. Ich freue mich, dass der vorherige Artikel Ihr Interesse geweckt hat, und ich werde versuchen, dies beizubehalten.
In dieser Folge werden wir uns auf die einfachste Variante konzentrieren - den Rohrmast, der eine Ebene unterhalb der Antenne abgespannt wird. Diese Situation ist in Abbildung 1 dargestellt. Um die Berechnungen zu vereinfachen, gehen wir davon aus, dass der gesamte Mast den gleichen Rohrdurchmesser und die gleichen Eigenschaften über seine gesamte Länge hat. Wir gehen auch davon aus, dass die Windgeschwindigkeit über die gesamte Länge des Mastes gleich ist (in Wirklichkeit ist sie knapp über dem Boden geringer).

Bei der Analyse der Größen und Eigenschaften, die sich auf das Verhalten des Systems auswirken, kommen wir zu dieser Liste
- Gesamthöhe des Mastes, Höhe des befestigten Seils, Abstand des Ankers vom Mastfuß (zur Ermittlung der auf das System wirkenden Kräfte)
- Außen- und Innendurchmesser des Rohrs (zur Bestimmung der Stärke und des Gewichts des Mastes)
- Physikalische Eigenschaften des Materials, aus dem das Rohr hergestellt ist: Dichte, Elastizitätsmodul, Festigkeitsgrenze, Proportionalitätsgrenze (zur Bestimmung der Festigkeit und des Gewichts des Mastes)
- Fläche und Gewicht der Antenne (zur Bestimmung der Windwiderstandskraft)
- Koeffizient des Widerstands des Mastes und der Antenne (zur Bestimmung der Windwiderstandskraft)
- Eigenschaften der Umgebung (Luft): kinetische Viskosität, Schwerkraftbeschleunigung, Luftdichte
- Windgeschwindigkeit
Ergebnisse der Berechnungen, die wir erhalten möchten:
- Kraft in der Achse des Mastbodens (Wirkung auf den Aufstellpunkt des Mastbodens)
- Kraft in der Seilachse (zur Auswahl des geeigneten Seils)
Wir werden uns jedoch vor allem für die Sicherheit interessieren - ob der Mast überleben wird und wie sicher er ist.
Aber wie soll man Sicherheit bewerten und vergleichen, wenn sie keine Einheit hat und ihr Ausdruck in Worten recht schwierig und vor allem subjektiv ist? Wir werden wahrscheinlich nicht in der Lage sein, sie zu messen. Der Bausektor verwendet eine Einheit namens Sicherheitskoeffizient.Er wird für jede Art von Bauwerk anders berechnet, aber seine Interpretation (Sinn) ist immer gleich: Ist er größer als 1, "besteht eine theoretische Garantie, dass das Bauwerk überleben wird". Der empfohlene Mindestwert ist 1,4. Wenn die Sicherheit des Bauwerks mehrere Faktoren umfasst, wird der Koeffizient für jeden Faktor separat berechnet, und die Gesamtsicherheit des Bauwerks ist der kleinste dieser Faktoren. In unserem Fall gibt es zwei kritische Faktoren: die Festigkeit des Materials, aus dem der Mast besteht (d. h. die Spannung in ihm), und das Knicken des Mastes (damit sich der Mast nicht verbiegt). Unsere Überlegungen führen zu einer Bewertung der Gesamtsicherheit des Systems.
Aus den vorangegangenen Ausführungen wird deutlich, dass es eine große Anzahl von Größen gibt, die für bestimmte Situationen unterschiedlich sind. Jeder hat eine andere Antenne, einen anderen Mast, eine andere Masthöhe ... Zur Veranschaulichung habe ich mehrere Situationen ausgewählt, die mir zur Demonstration geeignet erscheinen, und für die ich verschiedene Ergebnisse berechnet habe. In jedem Fall habe ich die Höhe der Seilbefestigung so gewählt, dass die Gesamtsicherheit am größten ist. Die einzelnen Varianten sind wie folgt:
- Die Masthöhe von 13 m, auf der eine ECO-Antenne angebracht ist (3el. Tribander für 10/15/20m). Diese Version ist für 3 verschiedene Masten berechnet: Rohrdurchmesser 80 mm mit 3 mm Wandstärke aus Duraluminium mittlerer Qualität (Ver. A), Rohr aus demselben Material 100/4 mm (B) und Stahlrohr 60/3 mm (C).
- Die Masthöhe von 13 m mit 11el. Antenne für ein 2 m-Band in zwei Versionen: durchschnittlich Duralumin 60 mm im Durchmesser mit einer 2 mm dicken Wand (D) und Glasfaser 60 mm im Durchmesser mit einer 5 mm dicken Wand (E).
- Bei der letzten Version handelt es sich um einen 23-Meter-Mast mit einer voluminösen Antenne TH7DX (7el. Tribander für 10/15/20m), ebenfalls in 2 Versionen: Hochwertiges Duraluminium mit 100 mm Durchmesser und einer Wandstärke von 10 mm (F) und Stahl mit 100 mm Durchmesser und einer Wandstärke von 5 mm (G).
Weitere für die Berechnungen verwendete Parameter sind: Luftdichte = 1,2 kg/m3, Erdbeschleunigung = 9,82 m/s2, Windgeschwindigkeit = 36 m/s = 130 km/h, Koeffizient des Mast- und Antennenwiderstands C = 1,2. Die Ergebnisse sind in Tabelle Nr. 1.
| Menge | Symbol | A | B | C | D | E | F | G | Einheit | |
| 11m duralumin ECO | 11m duralumin ECO |
11m Stahl ECO |
11m duralumin 11el. 2m | 11m Fibreglas11el. 2m | 23m duralumin TH7DX |
23m StahlTH7DX |
||||
| Mast - Rohr | ||||||||||
| Gesamthöhe | h | 13 | 13 | 13 | 13 | 13 | 23 | 23 | m | |
| Höhe der Seilbefestigung | h_ki | 12 | 12 | 12 | 11 | 9 | 17 | 20 | m | |
| Abstandshalter | r_ki | 10 | 10 | 10 | 10 | 10 | 15 | 15 | m | |
| Außendurchmesser | D_o | 80 | 100 | 60 | 60 | 60 | 100 | 100 | mm | |
| Innendurchmesser | D_i | 74 | 92 | 54 | 56 | 50 | 80 | 90 | mm | |
| Mastdichte | ro_s | 2700 | 2700 | 7850 | 2800 | 1200 | 2800 | 7850 | kg/m3 | |
| Elastizitätsmodul | E_s | 60000 | 60000 | 200000 | 60000 | 18000 | 60000 | 200000 | MPa | |
| Stärkegrenze | sigma_t | 300 | 300 | 320 | 300 | 220 | 350 | 320 | MPa | |
| Proportionalitätsgrenze | sigma_tu | 200 | 200 | 120 | 200 | 200 | 200 | 120 | MPa | |
| Seilreaktion | F_ropex | 1355 | 1486 | 1223 | 629 | 768 | 2446 | 2079 | N | |
| Reaktion im Mastboden | F_Kräfte in der Achse des Mastes | 2023 | 2346 | 2153 | 856 | 858 | 4951 | 5808 | N | |
| Reaktion im Mastboden senkrecht | F_Kräfte | -381 | -492 | -270 | -267 | -128 | -376 | -743 | N | |
| Kraft in der Seilachse | F_Seil | 2116 | 2321 | 1911 | 934 | 1034 | 3697 | 3466 | N | |
| Antenna | ||||||||||
| Antennenbereich | S_ant | 0,82 | 0,82 | 0,82 | 0,18 | 0,18 | 0,9 | 0,9 | m2 | |
| Antennengewicht | m_ant | 15 | 15 | 15 | 3,5 | 3,5 | 40 | 40 | kg | |
| Bewertung der Sicherheit | ||||||||||
| Spannung im Mast | k_t | 4,01 | 6,21 | 2,86 | 2,37 | 2,14 | 3,16 | 3,34 | ||
| Knick | k_b | 2,47 | 5,84 | 3,62 | 2,01 | 1,89 | 3,27 | 4,75 | ||
| völlige Sicherheit | k | 2,47 | 5,84 | 2,86 | 2,01 | 1,89 | 3,16 | 3,34 | ||
In der Version (A) wollte ich zeigen, dass trotz der Verwendung eines relativ dicken Rohrs die Gesamtsicherheit nicht so perfekt ist, wie manche aufgrund ihrer Erfahrung erwarten. Das liegt daran, dass die Anordnung des Systems mit einer einzigen Abspannhöhe definitiv nicht optimal ist und hohe Anforderungen an die Festigkeit des Mastmaterials stellt. Wir werden das nächste Mal über andere Versionen sprechen, aber ich kann verraten, dass die Festigkeit des Systems bei doppelter Abspannung viermal und bei dreifacher Abspannung sogar neunmal so hoch ist (natürlich nur, wenn sie in optimaler Höhe angebracht sind). Ich habe auch die Version (E) aufgenommen, weil ich gesehen habe, dass ähnliche Masten von mehreren Funkamateuren verwendet werden.
| Material | Dichte | Elastizitätsmodul | Stärkegrenze | Proportionalitätsgrenze |
| kg/m3 | MPa | MPa | MPa | |
| duralumin | 2800 | 60000 | 180-450 | x |
| aluminum | 2700 | 60000 | 60-150 | x |
| steel | 7850 | 200000 | 320-835 | 120-290 |
| Fiberglas | 1200 | 18000 | 220 | x |
Tabelle Nr. 2: Physikalische Eigenschaften der Materialien
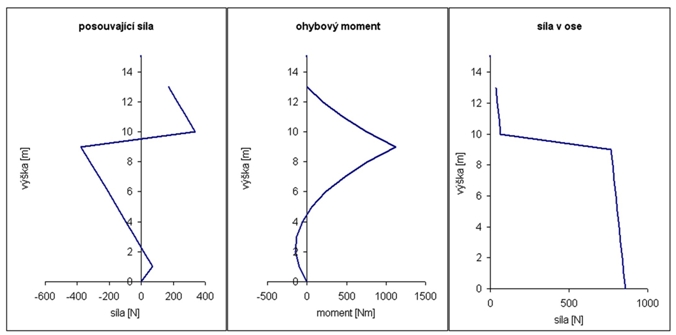
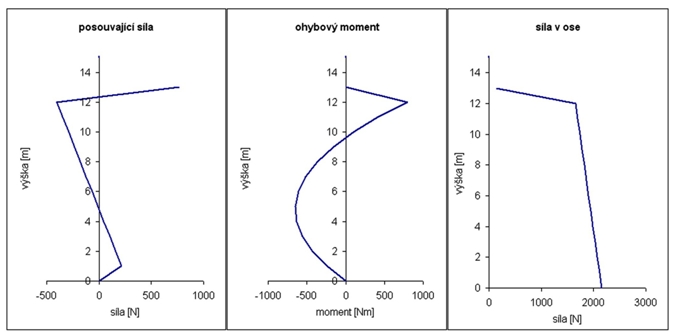
Neben dem eigenen Sicherheitssystem ist es auch interessant, die Verteilung einiger Größen über die Länge des Mastes zu betrachten. Dies ist in Abbildung 2 (für Version C) und 3 (E) dargestellt. Wenn die Abspannhöhe so gewählt wird, dass die Sicherheit maximiert wird, dann sind die Kurvenverläufe sehr ähnlich - deshalb zeige ich nur 2 typische Beispiele.

Die Grundlage der einfachen Methode ist einfach: Sie fassen das Seil in der Mitte zwischen zwei Punkten und ziehen es seitwärts, um eine bestimmte Auslenkung zu erreichen. Messen Sie die Kraft, die erforderlich ist, um diese Auslenkung zu erreichen (z. B. mit einer Federwaage). Je größer die Kraft ist, die erforderlich ist, um die gleiche Auslenkung zu erreichen, desto größer ist die Spannung (was offensichtlich ist).
Sie können die Spannung auch berechnen:
- Abstand zwischen den Punkten des Seils: L [mm]
- Auslenkung: D [mm]
- Zugkraft: F [N]
- Zugkraft: T [N]
T = F * L / D / 4
Die Formel ist einigermaßen genau, wenn der Abstand zwischen den Punkten viel größer ist als die Verschiebung (L >> D).
Hier ist eines der vielen Instrumente, die auf diesem Prinzip basieren:

Es gibt viele verschiedene Messgeräte auf dem Markt, zum Beispiel dieses von Loos&co. Seien Sie vorsichtig, denn diese Spanner sind für Stahlseile kalibriert, nicht für Kunststoffseile. Die Messgeräte für Stahlseile haben normalerweise einen geringen Abstand zwischen den Messpunkten.
Ein guter Indikator für die Spannung des Seils ist sein Durchhang (natürlich nur, wenn alle Seile gleich lang sind und kein starker Wind weht).