Tips & Advice
Useful tips, tricks and advice

This general guide will show you how to effectively set the required length of the guyrope, tension it, and secure it for long-term installation.
The procedure is suitable both for the installation of simple masts and for large antenna systems with lattice towers.
- Unscrew the turnbuckle to the maximum length.
- Install the turnbuckle to the ground anchor.
- Thread the rope through the upper eye/thimble.
- Install the Loop Cleat Tensioner to its free end. Use CL234 for ropes 6 to 11 mm (1/4" to 1/2") or CL223 for ropes 3 to 6 mm (1/8" to 1/4").
- Set the required length of the guyrope or adjust its length gradually. Advantageously, you can use a cleat tensioner, and its easy sliding on the rope. The procedure will differ depending on the method of installation of the mast/tower and guyropes (lifting the folded mast from the ground, gradual extension of the telescopic mast, installation of the mast in parts, ...).
- In the working position (before the final tensioning), the tensioning part should look something like this:


- After completing the adjustment, tension the rope with a cleat tensioner.
- Install the rope clamp and tighten it firmly:


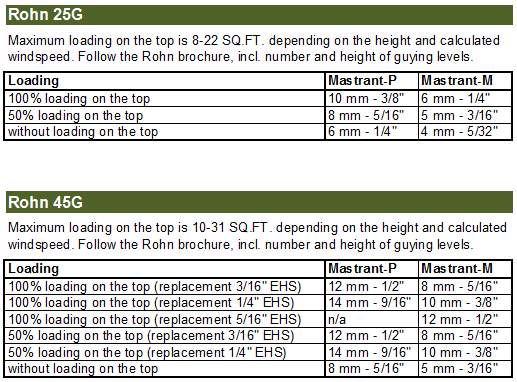
- You can now release the cleat tensioner and tie at least 2 safety knots (Double Half-hitch):

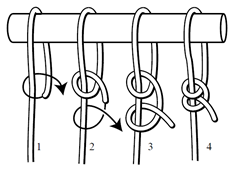
- Tighten the knots firmly and secure the free end of the rope with cable tape (for ropes up to approx. 5 mm - 3/16 ") ropes or install a second securing clamp.
- Tighten the guy rope to the required tension using a turnbuckle:


- Tighten the rope clamps firmly. If you use tensioners with lock nuts (like the jaw-jaw version on the picture), tighten these nuts as well.
- Before you begin, please read our articles Basic Instructions to Guy with Synthetic Ropes and Recommended Installation Procedure.

Suggested replacement of steel ropes by Mastrant synthetic ropes - based on strength only!
| Steel (1570 Mpa) | P | M |
| 4 mm (5/32") | 6 | 4 |
| 5 mm (3/16") | 8 | 5 |
| 6 mm (1/4") | 10 | 6 |
| 7 mm (9/32") | 12 | 8 |
| 8 mm (5/16") | 14 | 10 |
| 9 mm (11/32") | - | 12 |
| 10 mm (3/8") | - | 12 |
| Galvanized EHS | P | M |
| 5 mm (3/16") 1x7 | 10 | 6 |
| 6 mm (1/4") 1x7 | 14 | 8/10 |
| 8 mm (5/16") 1x7 | - | 12 |

When planning an “anchoring system” (guy-ropes with end termination, couplers and anchorage) there are a number of facts that have to be taken into account:
- The stability of the system is determined by its weakest link. That is why it is no use combining a rope of 5000 kg of strength with a turnbuckle 500 kg strong.
- Even the most excellent synthetic rope is elastic – when guyed it elongates. In the layout of the tower and its anchorage (even when fixing elements of the antennas) you have to reckon with this characteristic and always consider how the elongation of the anchoring system will affect the overall construction. In certain cases it will be necessary to use a stronger rope (with a smaller absolute extensibility), than for other constructions that are not negatively affected by the elongation of the anchors. A problem occurs especially in such a case, when the ground anchor point is situated too close to the tower base, or when dealing with a lattice tower with low flexibility.
- The rope must be screened against all kind of sharp edges. For this reason it is necessary to fix the rope with a thimble or tie it to a coupler with a very smooth surface. Be aware of the fact that inappropriate metallic materials corrode and therefore their surface roughens. Never should you tie a rope to a concrete slope or to a stone! If you do want to use a stone, a rock or a concrete slope as ground anchor point, we recommend using a loop from steel rope, which you can connect to the guy rope with the help of a smooth coupler.
- A great danger for any synthetic rope lies in friction against any object on its path. This can cause the rope to be seriously damaged or cut through, and has to be avoided at all cost. Even a guy rope on a tower can move enough to suffer friction damage if it touches anything along its length, so please locate your guys carefully. Particularly to be avoided are trees and tree branches. If you use tree support for a wire antenna, you must ensure that no part of the synthetic rope can get close enough to the tree to risk damage by rubbing. Always use steel rope near or in a tree. You could use a pulley on the end of a steel rope to keep the synthetic rope well clear.
- The lower part of the anchoring system can consist of steel rope cord in 2-4 meters of length. This ensures that the synthetic rope isn’t “chewed up” by an animal or gets damaged by some human activity (intentionally or unintentionally).
A key element of safety is the end termination of the rope:
- Guy ropes can be terminated with a thimble (permanent installation) or they can be tied to a smooth object.

- When fastening a rope by tying, we recommend making sure the rope does not move on the object it is tied to (even though we are talking about smooth fastening points). This can be achieved by tying the rope to a coupler – chain quick-acting coupler, spring hook or shackle – and only then fix it to the fastening point.
 We recommend Quadruple Half-hitch - it is the same as Double Half-hitch on following picture but four hitches.
We recommend Quadruple Half-hitch - it is the same as Double Half-hitch on following picture but four hitches.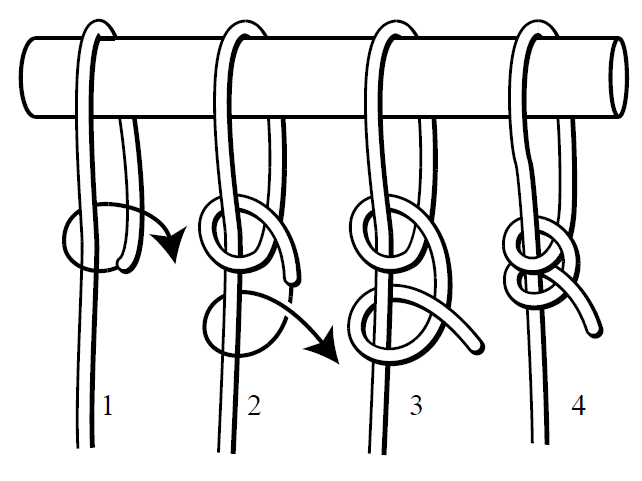
- Each thimble must be followed by a clip or swaged fitting. We recommend duplex wire rope clips or fist-grips (also called Deka). Behind the main clip (the one that follows the thimble) the loose end of the rope must be fixed by the knot (we recommend Double Half-hitch). Further, the end of the loose rope is insured against uncurling for example with a cable tie or bull-dog grips for thick ropes.


- Other possibility is using crimped terminals (swaged “clips”). Those are only practical on one end of the rope – otherwise it is not possible to adjust the length. We sell them as “Ready-made" or “Terminated” guyropes - here.

- When guyed, a rope’s diameter decreases and therefore it loosens inside the clip. For this reason, clips must be drawn up while the rope is guyed, that is “under pressure”.
- Beware of classic bull-dog grips! These rope clips are constructed specially for steel ropes and when under high tension they can “snip off” synthetic ropes. In no case do we recommend using them as main clips for the end termination of ropes – they may be used as “safety clips” behind the main clip, however.
Most common mistakes and accident causes:
- The anchor point is situated too near to the tower base and that is why the angle between the guy rope and the tower equals much less than 45 degrees.
- The clips weren’t re-tightened while the rope was under tension.
- Behind the clips there is no safety element (second clip, knot).
- The end of the rope is not terminated with a thimble, but tied directly to the construction.
- The rope was chewed through by an animal or cut through.
- In the following case there was used improper rope with high elongation.


- Calculate or measure the needed lengths of the guys (the part of the “anchoring system” made from the synthetic rope).
- Add the length needed for proper end termination. For the standard terminations (thimble, clip, knot) it is about 60-times the rope diameter for each end.
- Cut the rope using hot edge (for example with a soldering iron). Melting temperature of polyester is about 260 °C (500 °F), Dyneema 150 °C (300 °F).
- Prepare appropriate thimble. If needed, you can open the thimble by pliers, thread on the attaching subject and close it to original shape. Small shape distortion has no influence to total strength.
- Prepare appropriate clip – dismantle it.
- The rope wraps around the thimble, place it to the clip and put the clip together (see Figure). The open end of the rope should be left free, about 35-times the rope diameter (for the safety knot).

- Place the clip as close as possible to the thimble.
- Tighten the screws of the clip very firmly and make the knot (see Figure, we recommend Double Half-hitch). Fix the free end of the rope with a cable tie or rope clip (bull-dog grips are OK) to stop it fraying.


- It is necessary to tighten the clips repeatedly during tensioning the rope. Therefore at the inaccessible end of the guy is necessary to tighten before installing the guy. Attach the end of the rope (the one with the thimble) to a solid object and tighten the rope gradually. After each step (increase of tensioning force) tighten the screws of the clip. Ideally, the final tightening is performed at maximum workload (30% of the strength). With thicker ropes, however, this ideal is difficult to achieve – for example the stretching could be performed by a rope stretched between two fixed points and loading the rope perpendicular to the their axis with the required weight. Also we could use a car to pull on the rope or create a temporary hoist for tensioning.
- Place the guy where it will be used. Tension it gradually and tighten the clips (as described above).
- Visually check whether there has been slippage of the rope in the clip - if so, it means that we have not chosen a suitable tensioning and tightening procedure, or that the terminal is defective.
- For tensioning cables we can use threaded turnbuckles. For telescopic masts, we can do it without a turnbuckle. Lower the mast slightly and tighten clamps then wind the mast back up and retighten. The suitability of this procedure is, of course, different for each type of mast.
- Optimal pre-tension of the rope (tension in idle) is dependent on a number of factors - the design and strength of the mast, the type and strength of the rope, the distance from the base of the mast to the anchor point. In most applications best suited force is 5-20% of the strength of the rope. Do not guess! Calculate for your particular mast.
- After final tensioning of the guys in "idle" the rope will for some time continue "settling". Check the guys and, if necessary, tension them the next day after the installation and then about 3 times at intervals of about 1 week. We must always follow the correct procedure for tightening clamps!
Most common mistakes and accident causes:
- The anchor point is situated too near to the tower base and that is why the angle between the guy rope and the tower equals much less than 45 degrees.
- The clips weren’t re-tightened while the rope was under tension.
- Behind the clips there is no safety element (second clip, knot).
- The end of the rope is not terminated with a thimble, but tied directly to the construction.
- The rope was chewed through by an animal or cut through.
Martin Huml, OL5Y/OK1FUA,
During my radio amateur activities, I dedicate most of my time (probably like any one of us) to the question of antennas. And one of the most important and maybe the most challenging task is to get the antenna “into the air” and keep it there. Apparently this applies to all antennas, perhaps with the exception of beverage antennas... I wrote about this subject in the article “How to build and guy simple antenna masts” (magazine “Radioamatér” 2 & 3/2004). At that time, I already felt that this issue is so interesting, complicated and extensive that it would be appropriate to return to it.
Another motive for writing the following article was to include the questions asked either by my friends or emerging on their own, e.g. “Why are you guying the vertical so low down?”, “Will this rope be strong enough?”, “Will this mast be able to carry the antenna?” and so forth. Most of the time I couldn't find a better answer than “because I think it's enough” or “because I saw it somewhere like that”. This doesn't sound very scientific. Practice and experience are great and irreplaceable, but too much of it is guesswork, so when my activities brought me to “guying” I decided to look into it from the theoretical perspective as well. First, I would like to state that I am not an engineer; so, after studying some time, I consulted Engineer Richard Beber, who, unlike me, has studied this issue. Here, I would like to thank him - the article wouldn't have been written if it weren't for him.
Hence, as indicated by the name of this article, its main subject is focused on how to guy the antennas. This doesn't mean that owners of the self-standing masts won't find something interesting. For instance, calculations of forces acting on the antenna in the wind or other matters might be useful.
Used terms and simplification
I ask the experts and linguists for leniency - I use these terms as I know them from amateur practice:
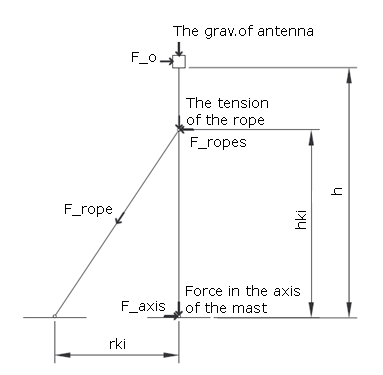
- Place (point) of mounting = the place where the guy rope is mounted (attached) on the mast
- Height of mounting = the distance between the point of mounting and the mast bottom (base, labeled HKI)
- Groung anchor point (Guying point) = the place where the guy rope is attached to the ground (or other fixed point)
- Distance of guying = the distance between the guying point and the mast bottom (base, labeled RKI)
- The system = the mast with antenna
A vertical antenna is actually a mast without the antenna. Therefore, where it is not appropriate in the following text, I will not distinguish between these two types of antennas. In other words, e.g. the phrase “guying in the middle of the mast” will have to be understood as “guying in the middle of the vertical”.
Unless stated otherwise, we assume that the mast is built on a horizontal surface; therefore, the ground guying points and the mast bottom are at the same level, perpendicular to the axis of the mast. This is for simplicity - the reality definitely tends to be different. Therefore, the following text will indicate how to deal with the reality.
In our considerations, we also do not deal with the behaviour of the antenna itself - we assume that the antenna on the mast does not change.
And, finally, for those who are not friends with physics - we will talk a lot about force, whose unit is 1 N (Newton). For instance, if you lift a weight of 1 kg, the acting force on you is approximately 10N.
The Antenna and the Mast
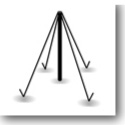
If we look at the simplified model of the guyed mast and the antenna at its top (fig. 1), the following forces will affect the system:
- gravity force (mass of the mast, ropes and antennas),
- resistant wind force,
- tension force of the guy ropes.
This set of forces will produce a reaction so that the resulting forces will be balanced. The reaction will appear in the gripping of the mast bottom and in the places of mounting of the guy ropes. There will also be a flexible deformation of the mast and the ropes. In this respect, we do not consider the irreversible deformation or destruction of the material - it is these cases that we want to avoid and therefore we will focus on the identification of all acting forces.
But forces do not represent all factors that will influence the behaviour of the system. We must not forget about the structure of the mast (tube, lattice structure etc.) and the material of which it is made, especially its physical properties such as density (specific gravity), flexibility and strength. Similarly, we need to know the properties of the guy ropes - their strength and elongation. Let's summarise what we need to know:
- antenna - mass
- antenna - shape (number, length and diameter elements)
- mast - structure, material
- guy rope - elongation (stretch at working load), strength
And the parameters with which we will be dealing are as follows:
- total height (the height of the antenna above ground = the height of the mast)
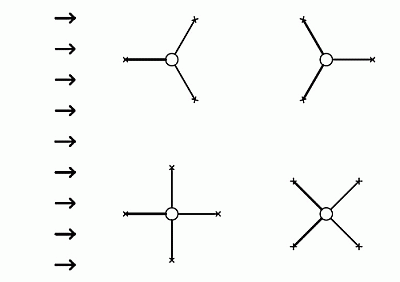
- the number of the guying directions (3 or 4)
- the number of guying levels (at how many levels will the mast be guyed)
- the height of the guy rope mounting(s)
- the distance of the guying point from the base
The distance of the guying
The first question that we will address is the influence of the distance of guying on the size of the forces (acting on the mast and the guy ropes). We will divide this task into the following marginal situations - in the first case, the wind is blowing from the guying direction; in the second case, the wind is blowing “in between the guys”. (fig. 2)
If the wind is blowing from the point of guying direction, it is a simple composition of forces - the case of a right triangle where one of the legs is the mast (h), the second one the distance between the mast bottom and the point of guying (r), where the guy rope is the hypotenuse (l). The proportion in which the individual legs of this triangle are is the proportion of forces acting in individual directions. We know (can calculate) the force Fant caused by the wind acting on the antenna. (Its specific value is not important at this moment; we will deal with it later - as we are now assessing the influence of the distance of the point of guying.) So the force on the mast (in its axis) is Fst = Fant * h / r, and the force acting on the guy rope is Fko = Fant * l / r. We will calculate the length of the rope by the Pythagorean Theorem: l = √(h2 + r2).
When the wind is blowing from the direction of the axis between the guys the situation is somewhat more complicated, because we have to bear in mind the angle between the guys - in other words, to how many directions the mast is guyed.
Guying directions
For this purpose we look at the mast from the top and introduce a total of 3 points - the mast and 2 guying points. Further we will introduce the direction from which the wind is blowing - it is the axis between the guying points going through the mast. The place where this axis intersects the connecting line between both of our guying points is a point that represents the virtual guying point for the calculation of acting forces. We see that it is much closer to the mast bottom than the guying distance - the closer it is, the larger the angle between the guys.
This is again a case of triangles, but not necessarily right angle triangles. If we apply the basic goniometric functions we get to these relations:
For 4 guys in 90°:
Fst = Fant * (h / r) * √2 = Fst = Fant * (h / r) * 1,414
Fko = Fant * (l / r) * (√2) / 2 = Fant * (l / )r * 0,707
For 3 guys in 120°:
Fst = Fant * (h / r) / cos(60/180π) = Fant * (h / r) / 0,5
Fko = Fant * (l / r) / cos(60/180π) = Fant * (l / )r .
At a first glance, an interesting feature might not be seen - when guying in 3 directions the force acting on the guy rope is the same as with wind “from the guy” as well as “in between the guys”.
How does this look in practice
From the theoretical perspective, which is probably boring for most of us, we move on to practical effects. (I promise that the following text will be without formulas - they would be much more complicated ...)
For illustration, I chose a simple example - a mast 10 m high with a tribander (10/15/20m) on top. I repeat again – it is an example to show the impact of guying distance and the number of directions to which the mast is guyed.
Therefore we are not interested in the mast or rope properties. So - we let the wind blow on the tribander at 130 km/h. It can be approximately calculated that the wind's acting force is approximately 775N. How I got to this result will be explained in the next chapter; for now this result will do.
I will however mention a very important fact, i.e. that the force is proportional to square (squared) velocity (e.g. half velocity = quarter force; the force in the case of 80 km/hour will thus be approx. 290 N). However, the force grows at a similar pace – so you can then understand what a tornado with its wind velocity reaching over 300 km/h in its centre can do, so please do not think that cars flying the air are a mere invention of the American filmmakers.
But now back to guying. In the following tables you will see the force calculated for both versions of guying (3 and 4 directions) and for the guying of 10 and 5 m. I think it is obvious that bringing the guying points closer to the mast results in unnecessary increase of the acting forces. This is similar in case of guying into 3 directions, which increases the load on the mast.
| High of the fixation | 10 m | ||
| Distance of guying points | 10 m | ||
| Speed of the wind | 130 km/h | ||
| Direction of the wind | number of directions | Force [N] effecting: | |
| guy-wire | mast | ||
| from direction of the guy-wire | 4 | 1 095 | 775 |
| between of the guy-wire | 4 | 775 | 1 095 |
| from direction of the guy-wire | 3 | 1 095 | 775 |
| between of the guy-wire | 3 | 1 095 | 1 245 |
| High of the fixation | 10 m | ||
| Distance of guying points | 5 m | ||
| Speed of the wind | 130 km/h | ||
| Direction of the wind | number of directions | Force [N] effecting: | |
| guy-wire | mast | ||
| from direction of the guy-wire | 4 | 1 732 | 1 549 |
| between of the guy-wire | 4 | 1 224 | 2 191 |
| from direction of the guy-wire | 3 | 1 732 | 1 549 |
| between of the guy-wire | 3 | 1 732 | 3 098 |
As you can see, given a sensible layout, forces caused by such high wind are not so huge. In other words - we do not need any extreme ropes for guying such an antenna. As can be found in a lot of places, even a relatively weak rope will endure if it’s designated for this purpose. The weakest places are all joints ... And in our conditions, we must not forget situations where the antenna is encased with icing... But this is really a distraction here and we will return to it.
Just to complete, one more paragraph - observant readers have definitely noticed that it is not about absolute height and distance - we will get the same results with mast of 20m and the distance of 20 and 10m. It is the angle formed between the guy rope and the mast. This should be acknowledged especially in situations where the guying point cannot be placed at a level perpendicular to the mast (it is on a slope). In such case, for example, if you had to place the guying point 3m lower than the mast bottom and you want to keep the angle between the rope and the mast 45° you have to place the guying point 13m from the axis of the mast (be careful, not from the mast bottom!). This can be hardly calculated at times, that is why it is possible to calculate and measure the length of the guying rope - in this case being 13*1,41 = 18.3m (1,41 = √2).
Wind force
If we place an object in the fluid stream, in our case the air, it will cause resistance by the friction and pressure elements. This resistance is determined experimentally in aerodynamic wind tunnels and is expressed in relation to the resistance force:
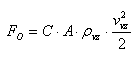 ,
,
where FO is the resistance force [N], C is the resistance coefficient of the object (-), A is the area of the object perpendicular to the wind direction [m2], ρvz is the air density [kg/m3], &vvz is the wind velocity [m/s].
The value of the resistance coefficient is not constant, but depends on the so-called Reynold's number - non-dimensional criterion, expressing the ratio of inertial and viscous
Re = vvz * d / v ,
where d is the characteristic dimension [m] a v is the kinematic viscosity of the air.
If we simplify the antenna (in our case a tribander) to several cylinders, then the characteristic dimension is the diameter and Re equals roughly 104 in normal conditions while the resistance coefficient of the object C is approximately 1.2. By the resistance force acting on the antenna (tube diameter d = 35 mm, length l = 23.6 m, wind velocity vvz = 36 m/s = 130 km/h; air density 1.2 kg/m3) we can determine:
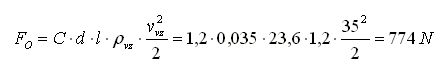 .
.
This force acts as a continuous load on the whole antenna (if we simplify the actual situation on the same velocity profile for the whole surface of the antenna). We can determine the resistance force acting on the mast in a similar way.
The following table illustrates forces calculated for several typical antennas (I apologize to those who can’t find their exact antenna in the table, please just extrapolate).
| Antenna | Wind area [m2] | Force of the wind [N] at speed as [km/h] | ||
| 50 | 130 | 180 | ||
| HF - 3el. tribander ECO | 0,82 | 116 | 765 | 1476 |
| HF - 3el. tribander A3S | 0,40 | 56 | 373 | 720 |
| HF - 3el. tribander TH3JRS | 0,32 | 45 | 299 | 576 |
| HF - 7el. tribander TH7DX | 0,88 | 124 | 821 | 1584 |
| HF - 11el. 5-bander TH11DX | 1,17 | 165 | 1092 | 2106 |
| HF - 10el. LP 10-30m LP1010 | 1,49 | 210 | 1390 | 2682 |
| HF - 5el. for 6m F9FT | 0,13 | 18 | 121 | 234 |
| HF - 5el. for 10m LJ105CA | 0,37 | 52 | 345 | 666 |
| HF - 5el. for 15m LJ155CA | 0,49 | 69 | 457 | 882 |
| HF - 5el. for 20m LJ205CA | 0,84 | 119 | 784 | 1512 |
| HF - 6el. for 20m HD OWA | 1,80 | 254 | 1680 | 3240 |
| HF - vertical 6-20m R6000 | 0,14 | 20 | 131 | 252 |
| HF - vertical 6-40m R8 | 0,24 | 34 | 224 | 432 |
| HF - Inv.V full-size 20-160m | 0,90 | 127 | 840 | 1620 |
| 2m - 9el. 2M9 | 0,12 | 17 | 112 | 216 |
| 2m - 11el. F9FT | 0,18 | 25 | 168 | 324 |
| 2m - 12el. 2M12 | 0,14 | 20 | 131 | 252 |
| 2m - 17el. F9FT | 0,29 | 41 | 271 | 522 |
| 2m - 18el. 2M18XXX | 0,30 | 42 | 280 | 540 |
| 70cm - 18el. 440-18 | 0,08 | 11 | 75 | 144 |
| 70cm - 21el. 440-21ATV | 0,12 | 17 | 112 | 216 |
| 70cm - 38el. 432-13WLA | 0,24 | 34 | 224 | 432 |
| 23cm - 35el. 23CM35EZ | 0,06 | 8 | 56 | 108 |
What can be caused by frost?
The frost, which is a very important element in our calculations, affecting the function (as well as survival) of the antenna, causes
- increase of the surface the wind effects and
- mass gain.
Because I do not have any personal experience with the frost I have consulted this issue with a few friends who have their antennas on a variety of problematic places including those where the frost lasts several months. Their experience indicates that frost on the components adds up to 50-100 % and in extreme cases up to 200 % to their original diameter (the component then increases its diameter). Let’s see how much this increases wind loading.
The previous chapter shows that the resistance force of the wind is directly proportional to the surface of the antenna perpendicular to the wind direction and, therefore, to the diameter of its components. So if the diameter of the components increases 2x, it doubles the wind force. These are very easy calculations - if you wish to design an antenna system for extreme frost, multiply the forces by 3.
The mass issue is more complicated. For its calculation, we need to know not only the thickness of the frost but also its density. Although the density of ice is 917 kg/m3, the density of frost stated in literature and standards is considered 400-500 kg/m3 - let 's calculate preferably 500 kg/m3. Since we are interested in the amount of increase of the mass of the standing antenna, we also need to know the density of the material, which it is made from. This is usually some aluminium alloy whose density is around 2800 kg/m3.
A brief remark about the calculation: for the sake of simplicity, we would again consider an antenna consisting of tubes or rods. The mass of the object m = V * ρ, where V is the volume and ρ the density. The volume of the cylinder is V = π * r2 * l, where r is the radius and l the length. If we substitute the known values we will calculate the original mass and the mass of the frost. This is demonstrated below.
| Design of element /boom | Multiplication of weight with icing: | ||
| 50% | 100% | 200% | |
| Spar (all diameters) | 1,2 | 1,5 | 2,4 |
| Pipe ø 8 mm, wall 1 mm | 1,5 | 2,2 | 4,3 |
| Pipe ø 10 mm, wall 1 mm | 1,6 | 2,5 | 5,0 |
| Pipe ø 14 mm, wall 1 mm | 1,8 | 3,0 | 6,4 |
| Pipe ø 24 mm, wall 1 mm | 2,4 | 4,4 | 9,9 |
| Pipe ø 24 mm, wall 2 mm | 1,7 | 2,8 | 5,7 |
| Pipe ø 30 mm, wall 1 mm | 2,7 | 5,2 | 12,1 |
| Pipe ø 30 mm, wall 2 mm | 1,9 | 3,2 | 6,7 |
| Pipe ø 50 mm, wall 1 mm | 3,8 | 7,8 | 19,2 |
| Pipe ø 50 mm, wall 2 mm | 2,5 | 4,5 | 10,3 |
The facts shown in the table may be shocking for some people. It is not easy to admit that the antenna consisting, for example, of tubes with 24mm in diameter with 1mm wall increases its mass in a 100% frost by 4.4 times! On the other hand, it is necessary to consider that the conditions for creating continuous frost on the entire perimeter of the tube, especially on those with larger diameters, are relatively rare in ordinary QTHs.
As a matter of interest, Wikipedia states the following about frost:
The frost is an atmospheric phenomenon that develops by creating ice crystals on the surface of the object by inflicting the following effects:
• freezing tiny droplets of the air's humidity (clouds, fog etc.) in it's contact with the surface of the ground, object or other subjects at the temperature of 0°C and below;
• precipitation (sublimation) of air's humidity on a sufficiently cold surface of the ground or subjects and that even without the presence of fog or clouds.
The highest probability of frost creation is with contact at a temperature (0 to -4 °C) between the surface of the object and the moist airflow. With temperature below -4 °C the possibility of frost creation decreases and at temperatures below -12 °C frost does not occur or is very weak.
The above data is interesting especially in the consideration of structure & design of the antenna - to what extent the components and the boom should be dimensioned and reinforced to avoid bending. That is again a completely different topic.
Next time, we will focus on guying a real mast, including considerations about its strength and other influencing elements.

Martin Huml, OL5Y/OK1FUA,
In the first part we talked about forces and the issues regarding guying in general; today we will talk about the mast itself. Before I begin I would like to thank for all your feedback, questions and other topics. I am glad that you were interested in the previous article and I will try to keep it that way.
In this sequel we will focus on the most basic version – the tube mast guyed in one level below the antenna. This situation is illustrated under figure 1. To simplify the calculations, we assume that the entire mast is the same tube diameter and has the same properties throughout its length. We will also assume that the wind velocity along the length of the mast is the same (in reality it is lower just above the ground).

When analyzing quantities and properties that affect the behavior of the system we get to this list:
- the total height of the mast, height of the attached rope, distance of the anchor from the mast bottom (to determine forces affecting the system)
- external and internal diameters of the tube (to determine the strength and the weight of the mast)
- physical properties of the material from which the tube is made from: density, elastic modulus, strength limit, proportional limit (to determine the strength and weight of the mast)
- area and weight of the antenna (to determine the wind resistance force)
- coefficient of the resistance of the mast and the antenna (to determine the wind resistance force)
- properties of the environment (air): kinetic viscosity, gravitation acceleration, air density
- wind velocity
Outputs of the calculations we wish to obtain:
- force in the axis of the mast bottom (action on the point of placement of the mast bottom)
- force in the axis of the rope (for the selection of the suitable rope)
However, we will be interested particularly in safety - if the mast will survive and to what degree of safety.
But how to assess and compare safety if it has no unit and its expression in words is quite difficult and above all subjective? We will be probably unable to measure it. Construction sectors use a unit called safety coefficient. It is calculated differently for each type of structure, but its interpretation (sense) is always the same: If it is greater than 1, “there is a theoretical guarantee that the structure will survive”. The recommended minimum value is 1.4. If the safety of the structure involves several factors, the coefficient is calculated for each factor separately and the total safety of the structure is the smallest one of them. In our case, there are two critical factors: the strength of the material of which the mast is made (i.e. the tension in it), and the mast buckling (so the mast will not bend). Our considerations will result in the assessment of the total safety of the system.
From the foregoing, it is clear that there are a large number of quantities that are different for specific situations. Everybody has a different antenna, different mast, different mast height ... For illustration I have chosen several situations, that I find appropriate for demonstration and for which I calculated different outputs. In each case I chose the height of the rope attachment so that the total safety is the greatest. Individual variations are as follows:
- The mast height of 13 m, on which an ECO antenna is placed (3el. tribander for 10/15/20m). This version is calculated for 3 different masts: tube diameter 80 mm with 3 mm thick wall from an average quality duralumin (ver. A), tube from the same material 100/4 mm (B) and steel tube 60/3 mm (C).
- The mast height of 13 m with 11el. antenna for a 2 m band in two versions: average duralumin 60 mm in diameter with a 2 mm thick wall (D) and fiberglass 60 mm in diameter with a 5 mm thick wall (E).
- The last version is a 23 m mast with a bulky antenna TH7DX (7el. tribander for 10/15/20m) again in 2 versions: high quality duralumin 100 mm in diameter with a 10 mm thick wall (F) and steel 100 mm in diameter with a 5 mm thick wall (G).
Other parameters used for calculations are: air density = 1.2 kg/m3, gravity acceleration = 9.82 m/s2, wind velocity = 36 m/s = 130 km/h, coefficient of mast and antenna resistance C = 1.2. The results are shown in table no. 1.
| Quantity | Symbol | A | B | C | D | E | F | G | Unit | |
| 11m duralumin ECO | 11m duralumin ECO |
11m steel ECO |
11m duralumin 11el. 2m | 11m fibreglass11el. 2m | 23m duralumin TH7DX |
23m steelTH7DX |
||||
| mast - tube | ||||||||||
| total height | h | 13 | 13 | 13 | 13 | 13 | 23 | 23 | m | |
| height of rope attachment | h_ki | 12 | 12 | 12 | 11 | 9 | 17 | 20 | m | |
| guy distance | r_ki | 10 | 10 | 10 | 10 | 10 | 15 | 15 | m | |
| external diameter | D_o | 80 | 100 | 60 | 60 | 60 | 100 | 100 | mm | |
| internal diameter | D_i | 74 | 92 | 54 | 56 | 50 | 80 | 90 | mm | |
| mast density | ro_s | 2700 | 2700 | 7850 | 2800 | 1200 | 2800 | 7850 | kg/m3 | |
| elastic modulus | E_s | 60000 | 60000 | 200000 | 60000 | 18000 | 60000 | 200000 | MPa | |
| strength limit | sigma_t | 300 | 300 | 320 | 300 | 220 | 350 | 320 | MPa | |
| proportional limit | sigma_tu | 200 | 200 | 120 | 200 | 200 | 200 | 120 | MPa | |
| rope reaction | F_ropex | 1355 | 1486 | 1223 | 629 | 768 | 2446 | 2079 | N | |
| reaction in mast bottom | F_forces in the axis of the mast | 2023 | 2346 | 2153 | 856 | 858 | 4951 | 5808 | N | |
| reaction in mast bottom perpendicular | F_axis | -381 | -492 | -270 | -267 | -128 | -376 | -743 | N | |
| force in rope axis | F_rope | 2116 | 2321 | 1911 | 934 | 1034 | 3697 | 3466 | N | |
| antenna | ||||||||||
| area of antenna | S_ant | 0,82 | 0,82 | 0,82 | 0,18 | 0,18 | 0,9 | 0,9 | m2 | |
| weight of antenna | m_ant | 15 | 15 | 15 | 3,5 | 3,5 | 40 | 40 | kg | |
| assesing the safety | ||||||||||
| tension in the mast | k_t | 4,01 | 6,21 | 2,86 | 2,37 | 2,14 | 3,16 | 3,34 | ||
| buckling | k_b | 2,47 | 5,84 | 3,62 | 2,01 | 1,89 | 3,27 | 4,75 | ||
| total safety | k | 2,47 | 5,84 | 2,86 | 2,01 | 1,89 | 3,16 | 3,34 | ||
In version (A) I wanted to show that although a relatively thick tube is used the total safety is not as perfect as some might expect based on their experience. This is because the arrangement of the system with a single guy height is definitely not optimal and places high demands on the strength of the mast material. We will talk about other versions next time, but I can disclose that the strength of the system in dual guying is four times greater and even nine times greater in triple guying levels (of course, if they are placed in optimal heights). I have also included version (E) because I have seen similar masts being used by several radio amateurs.
| material | density | elastic modulus | strength limit | proportional limit |
| kg/m3 | MPa | MPa | MPa | |
| duralumin | 2800 | 60000 | 180-450 | x |
| aluminum | 2700 | 60000 | 60-150 | x |
| steel | 7850 | 200000 | 320-835 | 120-290 |
| fiberglass | 1200 | 18000 | 220 | x |
Table no. 2: physical properties of the materials
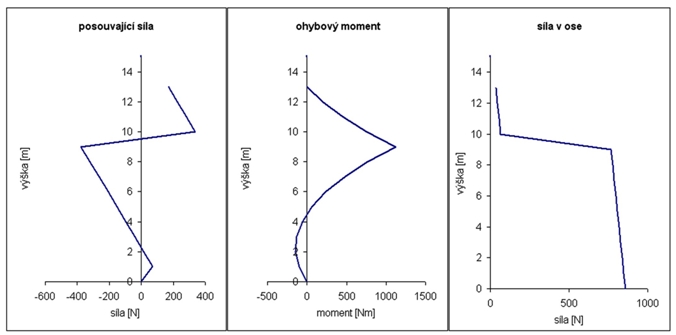
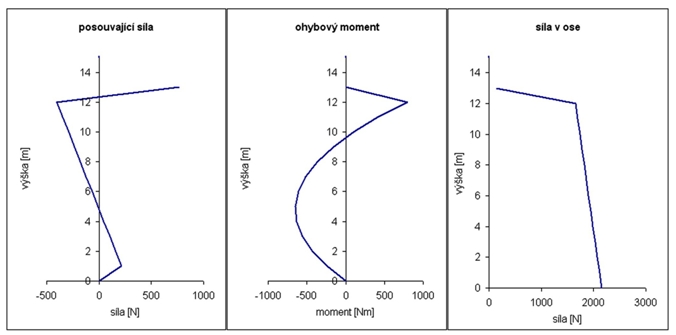
In addition to its own safety system, it is also interesting to look at the distribution of some quantities along the length of the mast. This is shown in figure 2 (for version C) and 3 (E). If the guying height is chosen at a height to maximize safety, then the curve shapes are very similar - that is why I show only 2 typical examples.

The basis of the simple method is easy: you grab the rope in the middle of two points and pull it sideways to get a certain displacement. Measure the force required to achieve this displacement (using a spring balance, for example). The greater the force required to achieve the same displacement, the greater the tension (which is obvious).
You can also calculate the tension:
- Distance between points on the rope: L [mm]
- Displacement: D [mm]
- Pulling force: F [N]
- Tensile force: T [N]
T = F * L / D / 4
The formula is reasonably accurate if the distance between the points is much greater than the displacement (L >> D).
Here is one of many instruments based on this principle:

There are many different measuring tools on the market, for example from Loos&co this one. Be careful because these tensioners are calibrated for steel ropes, not for synthetic ones. The gauges for steel ropes usually have a small distance between measuring points.
A good indicator of the tension in the rope is its sag (of course, if all ropes are the same length and there is no strong wind).