Martin Huml, OL5Y/OK1FUA,
Im ersten Teil haben wir über die Kräfte und die Probleme bei der Abspannung im Allgemeinen gesprochen; heute werden wir über den Mast selbst sprechen. Bevor ich beginne, möchte ich mich für all Ihr Feedback, Ihre Fragen und sonstigen Themen bedanken. Ich freue mich, dass der vorherige Artikel Ihr Interesse geweckt hat, und ich werde versuchen, dies beizubehalten.
In dieser Folge werden wir uns auf die einfachste Variante konzentrieren - den Rohrmast, der eine Ebene unterhalb der Antenne abgespannt wird. Diese Situation ist in Abbildung 1 dargestellt. Um die Berechnungen zu vereinfachen, gehen wir davon aus, dass der gesamte Mast den gleichen Rohrdurchmesser und die gleichen Eigenschaften über seine gesamte Länge hat. Wir gehen auch davon aus, dass die Windgeschwindigkeit über die gesamte Länge des Mastes gleich ist (in Wirklichkeit ist sie knapp über dem Boden geringer).
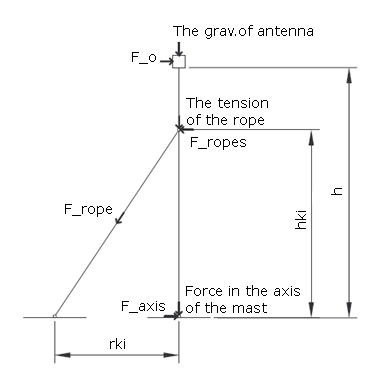
Bei der Analyse der Größen und Eigenschaften, die sich auf das Verhalten des Systems auswirken, kommen wir zu dieser Liste
- Gesamthöhe des Mastes, Höhe des befestigten Seils, Abstand des Ankers vom Mastfuß (zur Ermittlung der auf das System wirkenden Kräfte)
- Außen- und Innendurchmesser des Rohrs (zur Bestimmung der Stärke und des Gewichts des Mastes)
- Physikalische Eigenschaften des Materials, aus dem das Rohr hergestellt ist: Dichte, Elastizitätsmodul, Festigkeitsgrenze, Proportionalitätsgrenze (zur Bestimmung der Festigkeit und des Gewichts des Mastes)
- Fläche und Gewicht der Antenne (zur Bestimmung der Windwiderstandskraft)
- Koeffizient des Widerstands des Mastes und der Antenne (zur Bestimmung der Windwiderstandskraft)
- Eigenschaften der Umgebung (Luft): kinetische Viskosität, Schwerkraftbeschleunigung, Luftdichte
- Windgeschwindigkeit
Ergebnisse der Berechnungen, die wir erhalten möchten:
- Kraft in der Achse des Mastbodens (Wirkung auf den Aufstellpunkt des Mastbodens)
- Kraft in der Seilachse (zur Auswahl des geeigneten Seils)
Wir werden uns jedoch vor allem für die Sicherheit interessieren - ob der Mast überleben wird und wie sicher er ist.
Aber wie soll man Sicherheit bewerten und vergleichen, wenn sie keine Einheit hat und ihr Ausdruck in Worten recht schwierig und vor allem subjektiv ist? Wir werden wahrscheinlich nicht in der Lage sein, sie zu messen. Der Bausektor verwendet eine Einheit namens Sicherheitskoeffizient.Er wird für jede Art von Bauwerk anders berechnet, aber seine Interpretation (Sinn) ist immer gleich: Ist er größer als 1, "besteht eine theoretische Garantie, dass das Bauwerk überleben wird". Der empfohlene Mindestwert ist 1,4. Wenn die Sicherheit des Bauwerks mehrere Faktoren umfasst, wird der Koeffizient für jeden Faktor separat berechnet, und die Gesamtsicherheit des Bauwerks ist der kleinste dieser Faktoren. In unserem Fall gibt es zwei kritische Faktoren: die Festigkeit des Materials, aus dem der Mast besteht (d. h. die Spannung in ihm), und das Knicken des Mastes (damit sich der Mast nicht verbiegt). Unsere Überlegungen führen zu einer Bewertung der Gesamtsicherheit des Systems.
Aus den vorangegangenen Ausführungen wird deutlich, dass es eine große Anzahl von Größen gibt, die für bestimmte Situationen unterschiedlich sind. Jeder hat eine andere Antenne, einen anderen Mast, eine andere Masthöhe ... Zur Veranschaulichung habe ich mehrere Situationen ausgewählt, die mir zur Demonstration geeignet erscheinen, und für die ich verschiedene Ergebnisse berechnet habe. In jedem Fall habe ich die Höhe der Seilbefestigung so gewählt, dass die Gesamtsicherheit am größten ist. Die einzelnen Varianten sind wie folgt:
- Die Masthöhe von 13 m, auf der eine ECO-Antenne angebracht ist (3el. Tribander für 10/15/20m). Diese Version ist für 3 verschiedene Masten berechnet: Rohrdurchmesser 80 mm mit 3 mm Wandstärke aus Duraluminium mittlerer Qualität (Ver. A), Rohr aus demselben Material 100/4 mm (B) und Stahlrohr 60/3 mm (C).
- Die Masthöhe von 13 m mit 11el. Antenne für ein 2 m-Band in zwei Versionen: durchschnittlich Duralumin 60 mm im Durchmesser mit einer 2 mm dicken Wand (D) und Glasfaser 60 mm im Durchmesser mit einer 5 mm dicken Wand (E).
- Bei der letzten Version handelt es sich um einen 23-Meter-Mast mit einer voluminösen Antenne TH7DX (7el. Tribander für 10/15/20m), ebenfalls in 2 Versionen: Hochwertiges Duraluminium mit 100 mm Durchmesser und einer Wandstärke von 10 mm (F) und Stahl mit 100 mm Durchmesser und einer Wandstärke von 5 mm (G).
Weitere für die Berechnungen verwendete Parameter sind: Luftdichte = 1,2 kg/m3, Erdbeschleunigung = 9,82 m/s2, Windgeschwindigkeit = 36 m/s = 130 km/h, Koeffizient des Mast- und Antennenwiderstands C = 1,2. Die Ergebnisse sind in Tabelle Nr. 1.
| Menge | Symbol | A | B | C | D | E | F | G | Einheit | |
| 11m duralumin ECO | 11m duralumin ECO |
11m Stahl ECO |
11m duralumin 11el. 2m | 11m Fibreglas11el. 2m | 23m duralumin TH7DX |
23m StahlTH7DX |
||||
| Mast - Rohr | ||||||||||
| Gesamthöhe | h | 13 | 13 | 13 | 13 | 13 | 23 | 23 | m | |
| Höhe der Seilbefestigung | h_ki | 12 | 12 | 12 | 11 | 9 | 17 | 20 | m | |
| Abstandshalter | r_ki | 10 | 10 | 10 | 10 | 10 | 15 | 15 | m | |
| Außendurchmesser | D_o | 80 | 100 | 60 | 60 | 60 | 100 | 100 | mm | |
| Innendurchmesser | D_i | 74 | 92 | 54 | 56 | 50 | 80 | 90 | mm | |
| Mastdichte | ro_s | 2700 | 2700 | 7850 | 2800 | 1200 | 2800 | 7850 | kg/m3 | |
| Elastizitätsmodul | E_s | 60000 | 60000 | 200000 | 60000 | 18000 | 60000 | 200000 | MPa | |
| Stärkegrenze | sigma_t | 300 | 300 | 320 | 300 | 220 | 350 | 320 | MPa | |
| Proportionalitätsgrenze | sigma_tu | 200 | 200 | 120 | 200 | 200 | 200 | 120 | MPa | |
| Seilreaktion | F_ropex | 1355 | 1486 | 1223 | 629 | 768 | 2446 | 2079 | N | |
| Reaktion im Mastboden | F_Kräfte in der Achse des Mastes | 2023 | 2346 | 2153 | 856 | 858 | 4951 | 5808 | N | |
| Reaktion im Mastboden senkrecht | F_Kräfte | -381 | -492 | -270 | -267 | -128 | -376 | -743 | N | |
| Kraft in der Seilachse | F_Seil | 2116 | 2321 | 1911 | 934 | 1034 | 3697 | 3466 | N | |
| Antenna | ||||||||||
| Antennenbereich | S_ant | 0,82 | 0,82 | 0,82 | 0,18 | 0,18 | 0,9 | 0,9 | m2 | |
| Antennengewicht | m_ant | 15 | 15 | 15 | 3,5 | 3,5 | 40 | 40 | kg | |
| Bewertung der Sicherheit | ||||||||||
| Spannung im Mast | k_t | 4,01 | 6,21 | 2,86 | 2,37 | 2,14 | 3,16 | 3,34 | ||
| Knick | k_b | 2,47 | 5,84 | 3,62 | 2,01 | 1,89 | 3,27 | 4,75 | ||
| völlige Sicherheit | k | 2,47 | 5,84 | 2,86 | 2,01 | 1,89 | 3,16 | 3,34 | ||
In der Version (A) wollte ich zeigen, dass trotz der Verwendung eines relativ dicken Rohrs die Gesamtsicherheit nicht so perfekt ist, wie manche aufgrund ihrer Erfahrung erwarten. Das liegt daran, dass die Anordnung des Systems mit einer einzigen Abspannhöhe definitiv nicht optimal ist und hohe Anforderungen an die Festigkeit des Mastmaterials stellt. Wir werden das nächste Mal über andere Versionen sprechen, aber ich kann verraten, dass die Festigkeit des Systems bei doppelter Abspannung viermal und bei dreifacher Abspannung sogar neunmal so hoch ist (natürlich nur, wenn sie in optimaler Höhe angebracht sind). Ich habe auch die Version (E) aufgenommen, weil ich gesehen habe, dass ähnliche Masten von mehreren Funkamateuren verwendet werden.
| Material | Dichte | Elastizitätsmodul | Stärkegrenze | Proportionalitätsgrenze |
| kg/m3 | MPa | MPa | MPa | |
| duralumin | 2800 | 60000 | 180-450 | x |
| aluminum | 2700 | 60000 | 60-150 | x |
| steel | 7850 | 200000 | 320-835 | 120-290 |
| Fiberglas | 1200 | 18000 | 220 | x |
Tabelle Nr. 2: Physikalische Eigenschaften der Materialien
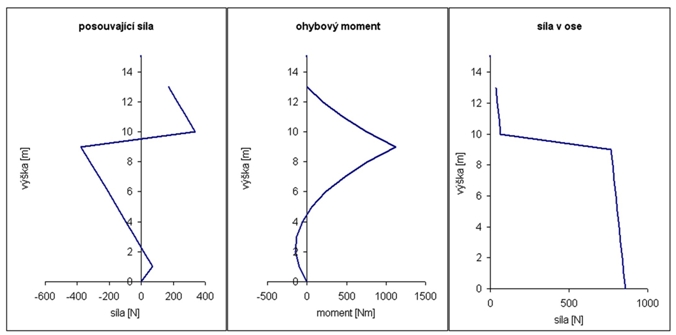
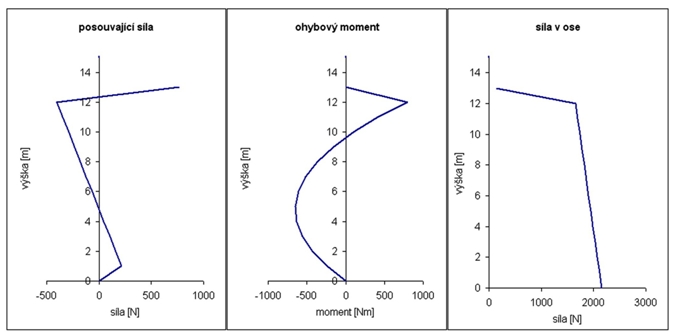
Neben dem eigenen Sicherheitssystem ist es auch interessant, die Verteilung einiger Größen über die Länge des Mastes zu betrachten. Dies ist in Abbildung 2 (für Version C) und 3 (E) dargestellt. Wenn die Abspannhöhe so gewählt wird, dass die Sicherheit maximiert wird, dann sind die Kurvenverläufe sehr ähnlich - deshalb zeige ich nur 2 typische Beispiele.