Martin Huml, OL5Y/OK1FUA,
V prvním díle jsme si něco řekli o silách a problematice kotvení obecně, dnes si začneme povídat o stožáru jako takovém. Ještě než začnu, chci poděkovat za všechny ohlasy, otázky a další náměty. Jsem rád, že vás článek zaujal a budu se snažit, aby tomu tak bylo i nadále.
V tomto pokračování se budeme věnovat nejzákladnější variantě - tedy trubkovému stožáru kotvenému v jedné úrovni pod anténou. Tato situace je znázorněna na obrázku 1. Pro zjednodušení výpočtů uvažujeme, že celý stožár je z trubky stejného průměru a stejných vlastností po celé délce. Rovněž budeme předpokládat, že rychlost větru je po celé délce stožáru stejná (ve skutečnosti bývá těsně nad zemí nižší).

Při rozboru veličin a vlastností, které mají vliv na chování soustavy, dojdeme k tomuto výčtu:
- celková výška stožáru, výška uchycení lana, vzdálenost kotvy od paty stožáru (pro určení sil, jež na soustavu působí)
- vnější a vnitřní průměr trubky (pro určení pevnosti a hmotnosti stožáru)
- fyzikální vlastnosti materiálu, ze kterého je trubka vyrobena: hustota, modul pružnosti, mez pevnosti, mez úměrnosti (pro určení pevnosti a hmotnosti stožáru)
- plocha a hmotnost antény (pro určení odporové síly větru)
- součinitel odporu stožáru a antény (pro určení odporové síly větru)
- vlastnosti prostředí (vzduchu): kinetická viskozita, gravitační zrychlení, hustota vzduchu
- rychlost větru
Výstupy výpočtů, jež nás budou zajímat:
- síla v ose stožáru v patě (působení na bod umístění paty stožáru)
- síla v ose lana (pro volbu vhodného lana)
Zajímat nás však bude především bezpečnost - zda stožár vydrží a s jakou mírou bezpečnosti.
Jak však posuzovat a porovnávat bezpečnost, když nemá žádnou jednotku a i její vyjádření slovy je poměrně obtížné a především subjektivní? Ani změřit pravděpodobně nepůjde. V konstruktérských odvětvích se používá veličina označovaná jako koeficient bezpečnosti. Ten se pro každý druh konstrukce vypočítává odlišně, jeho interpretace (smysl) je však vždy stejný: Pokud je větší než 1, „je teoretická jistota, že konstrukce vydrží". Doporučená minimální hodnota je 1,4. Pokud se na bezpečnosti konstrukce podílí více faktorů, počítá se její koeficient pro každý faktor zvlášť a celkovou bezpečností soustavy je ten nejmenší z nich. V našem případě jsou kritické faktory 2: pevnost materiálu, ze kterého je stožár vyroben (tedy napětí v něm) a vzpěr stožáru (aby se stožár neprohnul). Výsledkem našich úvah bude tedy posouzení celkové bezpečnosti soustavy.
Z výše uvedeného je zřejmé, že veličin, které jsou pro konkrétní situace různé, je velké množství. Každý má jinou anténu, jiný stožár, jinou výšku stožáru... Pro názornost jsem tedy vybral několik situací, které mi připadají vhodně ukázkové a pro něž jsem spočítal jednotlivé výstupy. Pro každý případ jsem zvolil takovou výšku uchycení lana, aby celková bezpečnost vycházela co největší. Jednotlivé varianty jsou tyto:
- Stožár výšky 13 m, na němž je umístěná anténa ECO (3el. tribander pro 10/15/20m). Tato varianta je spočítána pro 3 různé stožáry: trubka průměru 80 mm se sílou stěny 3 mm z průměrně kvalitního duralu (var. A), trubka ze stejného materiálu 100/4 mm (B) a ocelová trubka 60/3 mm (C).
- Stožár výšky 13 m s 11el. anténou pro pásmo 2 m ve 2 variantách: průměrný dural průměru 60 mm se stěnou 2 mm (D) a laminát průměru 60 mm se stěnou 5 mm (E).
- Poslední variantou je stožár vysoký 23 m s mohutnou anténou TH7DX (7el. tribander pro 10/15/20m) opět ve 2 variantách: kvalitní dural průměru 100 mm se stěnou 10 mm (F) a ocel průměru 100 mm se stěnou 5 mm (G).
Ostatní parametry použité pro výpočty jsou: hustota vzduchu = 1,2 kg/m3, gravitační zrychlení = 9,82 m/s2, rychlost větru = 36 m/s = 130 km/h, součinitel odporu stožáru a antény C = 1,2. Výsledky jsou uvedeny v tab. 1.
| Veličina | Symbol | A | B | C | D | E | F | G | Jednotka | |
|
11m |
11m dural ECO |
11m ocel ECO |
11m dural 11el. 2m | 11m laminát 11el. 2m | 23m dural TH7DX |
23m ocel TH7DX |
||||
| stožár - trubka | ||||||||||
| výška celková | h | 13 | 13 | 13 | 13 | 13 | 23 | 23 | m | |
| výška uchycení lana | h_ki | 12 | 12 | 12 | 11 | 9 | 17 | 20 | m | |
| vzdálenost kotvy | r_ki | 10 | 10 | 10 | 10 | 10 | 15 | 15 | m | |
| vnější průměr | D_o | 80 | 100 | 60 | 60 | 60 | 100 | 100 | mm | |
| vnitřní průměr | D_i | 74 | 92 | 54 | 56 | 50 | 80 | 90 | mm | |
| hustota stožáru | ro_s | 2700 | 2700 | 7850 | 2800 | 1200 | 2800 | 7850 | kg/m3 | |
| modul pružnosti | E_s | 60000 | 60000 | 200000 | 60000 | 18000 | 60000 | 200000 | MPa | |
| mez pevnosti | sigma_t | 300 | 300 | 320 | 300 | 220 | 350 | 320 | MPa | |
| mez úměrnosti | sigma_tu | 200 | 200 | 120 | 200 | 200 | 200 | 120 | MPa | |
| reakce lana | F_ropex | 1355 | 1486 | 1223 | 629 | 768 | 2446 | 2079 | N | |
| reakce v patě v ose | F_patoso | 2023 | 2346 | 2153 | 856 | 858 | 4951 | 5808 | N | |
| reakce v paté kolmá | F_pat | -381 | -492 | -270 | -267 | -128 | -376 | -743 | N | |
| síla v ose lana | F_lano | 2116 | 2321 | 1911 | 934 | 1034 | 3697 | 3466 | N | |
| anténa | ||||||||||
| plocha antény | S_ant | 0,82 | 0,82 | 0,82 | 0,18 | 0,18 | 0,9 | 0,9 | m2 | |
| hmotnost antény | m_ant | 15 | 15 | 15 | 3,5 | 3,5 | 40 | 40 | kg | |
| posouzení bezpečnosti | ||||||||||
| napětí ve stožáru | k_n | 4,01 | 6,21 | 2,86 | 2,37 | 2,14 | 3,16 | 3,34 | ||
| vzpěr | k_v | 2,47 | 5,84 | 3,62 | 2,01 | 1,89 | 3,27 | 4,75 | ||
| celková bezpečnost | k | 2,47 | 5,84 | 2,86 | 2,01 | 1,89 | 3,16 | 3,34 | ||
Na variantě (A) bych chtěl ukázat skutečnost, že přestože je použita poměrně silná trubka, celková bezpečnost není nijak oslnivá, jak možná někteří na základě zkušeností čekali. Je to dáno tím, že uspořádání sestavy s jedinou kotvící výškou není rozhodně optimální a klade vysoké nároky na pevnost materiálu stožáru. O jiných variantách si povíme příště, již teď vám ale prozradím, že pevnost soustavy při dvojím kotvení je čtyřnásobná a dokonce devítinásobná při 3 kotvicích úrovních (samozřejmě pokud jsou umístěny v optimálních výškách). Variantu (E) jsem zařadil proto, neboť jsem podobné stožáry viděl použité u některých radioamatérů.
| materiál | hustota | modul pružnosti | mez pevnosti | mez úměrnosti |
| kg/m3 | MPa | MPa | MPa | |
| dural | 2800 | 60000 | 180-450 | x |
| hliník | 2700 | 60000 | 60-150 | x |
| ocel | 7850 | 200000 | 320-835 | 120-290 |
| laminát | 1200 | 18000 | 220 | x |
Tab. 2: fyzikální vlastnosti materiálů
Kromě vlastní bezpečnosti soustavy je zajímavé podívat se i na rozložení některých veličin po délce stožáru. To ukazují obrázky 2 (pro variantu C) a 3 (E). Pokud je výška kotvení volena ve výšce pro dosažení co nevětší bezpečnosti, jsou tvary křivek velmi podobné - proto uvádím pouze 2 typické příklady. Pro přesnost ještě doplňuji, že veličiny jsou počítány po jednotlivých metrech a výslednými body je poté proložena křivka grafu.
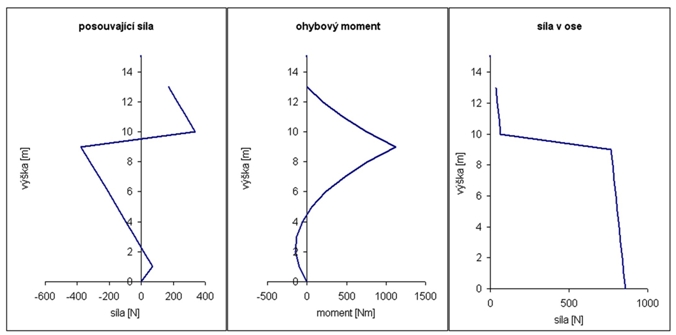
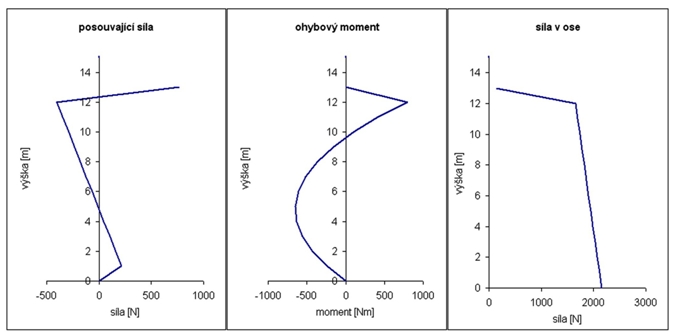
V příštím pokračování se budeme zabývat metodami, jak zvýšit pevnost (a tedy i bezpečnost) sestav, resp. jak optimalizovat konstrukci tak, aby byla sestava byla bezpečná a přitom co nejsnadněji realizovatelná.

